 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Расчет комплексного входного сопротивления цепи 12
КУРСОВАЯ РАБОТА
по дисциплине «Электротехника и электроника»
по теме «Расчет линейных электрических цепей с синусоидальным источником ЭДС с использованием символического метода»
Вариант №
Выполнил: студент группы РК-233 Иванов И.И.
Проверил: ассистент кафедры ТиОЭ Радченко А.В.
Омск 2016 Техническое задание к курсовой работе В электрической цепи (рис. 1), содержащей один источник электрической энергии напряжением 1. Определить комплексное входное сопротивление цепи. 2. Найти действующие и мгновенные значения токов во всех ветвях схемы. 3. Рассчитать действующие значения падений напряжений на всех элементах цепи. 4. Составить баланс мощностей. 5. Провести проверку расчетов по I и II законам Кирхгофа. 6. Построить топографическую векторную диаграмму токов и напряжений. При решении поставленных задач использовать символический метод расчета.
Рис. 1. Схема электрической цепи Параметры элементов электрической цепи заданы в таблице 1. Таблица 1
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Сущность символического метода расчета цепей синусоидального тока состоит в том, что для упрощения расчета переходят от решения уравнений для мгновенных значений токов и напряжений, являющихся интегро-дифференциальными уравнениями, к алгебраическим уравнениям в комплексной форме. При таких условиях расчет цепи удобнее вести для комплексных действующих величин синусоидальных токов и напряжений. В данной курсовой работе для определения токов и напряжений каждого элемента схемы, содержащей только один источник электрической энергии, следует использовать метод эквивалентных преобразований, поскольку известны сопротивления всех элементов цепи и ЭДС источника. Для решения такой задачи отдельные участки электрической цепи с последовательно или параллельно соединенными элементами заменяют одним эквивалентным комплексным сопротивлением, как показано на рисунке 2. Электрическую схему упрощают постепенным преобразованием отдельных участков и приводят к простейшей цепи, содержащей источник электрической энергии и эквивалентный пассивный элемент (рис. 3), включенный последовательно [1].
РАСЧЕТНАЯ ЧАСТЬ Расчет комплексного входного сопротивления цепи Вычисляем реактивные сопротивления элементов схемы:
Разбиваем схему на три участка по числу токов в ветвях (рис. 2) и рассчитываем комплексные сопротивления каждого участка (ветви).
Рис. 2. Схема замещения заданной цепи с эквивалентными комплексными сопротивлениями
Комплексные сопротивления участков цепи:
Рассчитываем эквивалентное комплексное сопротивление параллельных ветвей и преобразовываем схему в упрощенный вид, как показано на рис. 3.
Рис. 3. Схема замещения заданной цепи с эквивалентным преобразованием параллельных ветвей
Комплексное входное сопротивление цепи: ZΣ =Z1 + Z23 = 41 – j18,09 + 1,02 + j5,56 = 42,02 – j12,53 Ом.
12 |
, выполнить следующие действия:
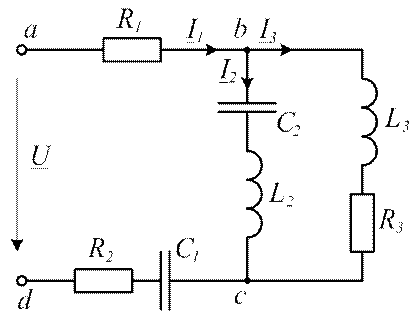
17,59 Ом;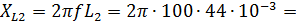
22,12 Ом;
18,09 Ом;
15,79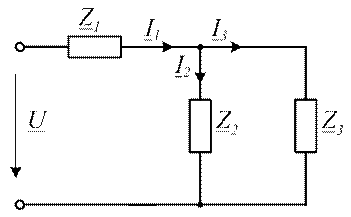 Ом.
Ом;
= 44,81e -j23,8º Ом;
Ом;
= 6,33e j90º Ом;
Ом;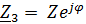
= 27,98e j26,7º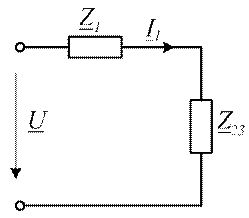 Ом.
Ом;
Ом.