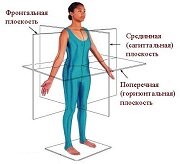
 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Рентгенді-фотоэлектронды спектроскопия.
Зерттелетін зат сынамасына рентген сәулесі түсіріледі. Осының нәтижесінде фотоэлектрондар ұшырылып шығарылады. Электрондар, негізінен, сыртқы қабаттардан жақсы ұшырылады. Қабат қалыңдаған сайын электрон ұшырылып шығарылуы төмендей береді. Бұл әдісті өзгеше "Химиялық талдаудың элетрондық спектроскопиясы " (Электронная спектроскопия химического анализа ЭСХА) деп те атайды. Электрондардың атом бойындағы байланыс беріктігіне қарай, олар әртүрлі кинетикалық энергиямен ұшып шығады. Осы шама бойьнша қай элемент екендігіне тұжырым жасалынады. Рентгенді-фотоэлектронды спектроскопия (РФЭС) - әдісімен сутегіден өзге элементтсрдің бәрін де анықтауға болады. РФЭС әдісімен - валенттілікті - тотығу дәрежесін - атом бойындағы заряд тығыздығын анықтауға болады. РФЭС әдісімен электр өткізгіштік қасиетке ие емес заттарды анықтау қиындық тудырады. Ал енді, осы РФЭС әдісіне керісінше, зерттелетін зат сынамасына электрондар ағынын шоғырландырсақ, онда атом бойының ішінде рентген сәулесінің түзілетінін білеміз. Түзілген рентген сәулесінің сын-сипатына қарай отырып оның кандай элемент екендігін, ал рентген сәулесінің интенсивтілігі арқылы оның қандай мөлшерде бар екендігін анықтауға болады. Электрон шоғыры сынама бетінің 200 нм-ге дейін тереңдігіне бойлай алады. Осының нәтижесінде зат беткі қабатында іздестіріліп отырған элементтің қандай дәрежеде таралғандығы туралы мәлімет алуға болады. Бұл электрондық микрозондәдісі деп аталады. Электрондықмикрозонд әдісімен катализатор құрамындағы промоторлардың орналасу ретіне талдау-тұжырым жасауға болады. Сонымен қатар, рентген сәулелерінің дифракциясы мөлшері 10 нм кіші бөлшектерді анықтауда тиімді. Бөлшектердің ауқымы 10 нм үлкен болған жағдайда олардың құрылымы туралы мәліметті "Метод протяженной тонкой структуры рентгеновского поглощения" – ПТРСП әдісі арқылы алуға болады. Бұл әдісте аморфты немесе кристалл заттардың жекелеген атомдарын немесе бірнеше элементті қатар бірге зерттеуге мүмкіндік бар. Аталған әдіс катализаторларды зерттеулерде қолданылады[5]. 3 Қатты денелер туралы 3.1 Атомдардың сызықтық спектрлері және бөлшектердің дифракциясы
Қыздырылған қатты денелер (сұйықтар және тығыз газдар) үздіксіз спектр түрінде сәулеленеді. Бұл сәулеленулер атомдар мен молекулалардың тербелістерінен болады. Сиретілген газдарды да қоздырып, оларды да сәуле шығартуға балады. Мұндай газдардың сәулелерінің спектрі үздіксіз емес, дискретті болады. Әрбір заттың тек өзіне ғана тән шығару спектрі болады. Шығару спектіріне қарап бір затты екінші заттан ажырата аламыз. Егер үздіксіз спектрі бар сәулелену газ арқылы өтетін болса, онда спектрде қара сызықтар пайда болады - олар жұтылу спектрі деп аталады. Газдардың қандай жиілікпен сәуле шығаратын болса, сондай жиілікте оны жұтатындығы анықталды. Газдардың дискреттік спектрі тек көрінетін облыста ғана емес, көрінбейтін, ультракүлгін және инфрақызыл облыстарда да беретіндігі белгілі. Сутегі ең қарапайым атом болып табылады: оның ядросының төңірегінде тек жалғыз электрон ғана айналып жүреді. Оның спектрі де ең қарапайым. Сутегі спектріндегі сызықтардың ара қашықтығы қарапайым заңға сай кемиді. 1885 жылы Дж. Дж. Бальмер сутегі спектріндегі көрінетін төрт сызықтың (656, 486, 434 және 410нм)
өрнегіне бағынатындығын көрсетті. Мұндағы R - Ридберг тұрақтысы (R=1,097·10
3.1 сурет. Сутегі спектріндегі Бальмер сериясы сызықтары
Сутегі спектрінің жүргізілген зертеулері УК және ИҚ облыстарда құрылымы Бальмердікіндей, бірақ толқын ұзындықтары басқа болатын тағы да сериялардың бар екендігін тапты. Лайман сериясы:
Пашен сериясы:
Брэкет сериясы:
Пфунд сериясы:
Онда жалпылама өрнек мына түрде беріледі:
(3.2) өрнегі Бальмердің біріккен өрнегі деп аталады. Егер деп белгілесек, онда сутегі атомының кез келген сызығының толқындық санын мынадай формуламен өрнектеуге болады:
мұндағы Т(
Бірақ Бор жүйелі атом теориясын барген жоқ, ол жаңа теорияның негізгі қағидаларын постулаттар түрінде тұжырымдады. I постулат. Атомдық система тек ерекше стационар немесе кванттық күйлерде ғана болады, олардың әр қайсысына белгілі бір энергия сәйкес келеді. Стационар күйде атом сәуле шығармайды. Бұл постулат классикалық электродинамика заңына қайшы. Себебі, ядроны айналғанда электрон қозғалысы үдемелі қозғалыс, ал үдемелі қозғалыстағы электрон электромагниттік толқын шығаруы және электрон энергиясы кез келген мәнге ие болуы керек. II постулат. Атом энергиясы көп
ал шығарылған сәуленің жиілігі:
Ал егер атом фотонды жұтатын болса, ол энергиясы аз III постулат (орбиталарды кванттау ережесі ). Атом стационар күйде болғанда электрон дөңгелек орбитамен қозғала отырып, импульс моменті үшін квантталған мәндері болуы керек:
мұнда n=1,2,3,...-орбитаның кванттық саны деп аталады; m-электрон массасы,
Электрон ядроны дөңгелек орбитамен айналады деп есептеп, Бор r -радиусымен қозғалған электронға Кулон күшімен центрге тартқыш күш әсер етеді деген
Z-атомдық нөмір,
Егер (2.5.3) теңдігінің екі жағын да квадраттасақ,
Ал
3.2 сурет. Орбиталар
және т.б. Алғашқы төрт орбита 3.2 суретте көрсетілген. Сәйкестік принціпі. Бордың классикалық көзқарастарға қайшы келетін бірқатар тоқтамдарды қабылдағандығын ерекше атап өту керек. Мәселен, ол, электрон рұқсат етілген орбиталармен үдемелі қозғалғанымен сәуле шығармайды деп және импульс моменті квантталады деп тоқтам жасады. Сонымен қатар, Бор бір энергетиқалық деңгейден екінші энергетикалық деңгейге өткенде электрон қалай қозғалады деген сұраққа жауап бере алмады. Алайда, атомдық электрондар әлеміндегі жағдай макроскопиялық денелер әлеміндегідей деп айтуға болмайды. Бірақ та Бор кванттық теория макроскопиялық әлеммен істес болатын жерлерде оның болжап айтқандары классикалық теория нәтижелерімен бірдей түсуі тиіс деген. Бұл оның сәйкестік принципінің мазмұны болып табылады. Сутегі атомының Бор ұсынған теориясында сәйкестік принципі орындалады. Ядролардан тым шалғай орналасқан макроскопиялық мөлшерлерге жуықтау орбиталар арасындағы кванттық өтулерді байқау қиын. Мұндай орбиталардың мөлшерлерін үздіксіз, макроскопиялық жағдайлардағыдай түрде өзгереді деуге болады.
3.3 сурет. Қозған күйлер Кванттық сандар. Атомның ішінде қозғалыстағы электронның күйін сипаттау үшін кванттық сандар қолданылады. Олардың саны төртеу. Атомдағы электронның энергиясын бас кванттық сан n арқылы сипаттайды, n=1,2,3,...бүтін сандарға тең болады да, электрон энергиясы үшін дискреттік мәндер береді. Екінші сан - орбиталдық кванттық сан
мұндаға p- электронның қозғалыс мөлшерінің моменті (импульс моменті). Сутек атомының ішіндегі қозғалыс мөлшерінің моменті мынаған тең:
Атомның орбиталық моделі 5.1.1-суретте берілген.
3.4сурет. Орбиталық модель
Үшінші сан - магниттік кванттық сан
Оның сан мәндері: Осы магниттік кванттық санның болуына байланысты атомның сыртқы магнит өрісіндегі энергия деңгейлері бірнеше қосымша деңгейлерге жіктеледі. Осындай құбылысты бірінші рет 1896 жылы голланд физигі П.Зееман байқаған, сондықтан бұл құбылыс Зееман эффектісі деп аталады. Күйдің энергиясы магнит өрісі бар кезде тек n санына ғана емес, сонымен қатар ml санына да тәуелді болады (3.5 сурет). «Магниттік кванттық сан» деген атау осыдан шыққан.
3.5 сурет.Магниттік кванттық сандар
Ал, негізгі энергетикалық деңгейлердің сыртқы электр өрісінде қосымша деңгейлерге жіктелуін неміс физигі И. Штарк (1874-1957) тәжірбие жүзінде ашқандықтан Штарк эффектісі деп аталады. Төртінші сан – спиндік кванттық сан S. Оны 5.2-де қарастырамыз. Бөлшектердің дифракциясы. Дэвисон-Джермер тәжірибелерінде кристалдардың бетінен электрондардың шағылуы зерттелген. Тәжірибенің схемасы 3.6 суретте көрсетілген.
3.6 сурет. Электрондардың шағылуы
Дэвисонның нобельдік лекциясынан үзінді келтірейік (Дэвисон мен Томсон электрондардың дифракциясын ашқан үшін Нобель сыйлығын алған): никель кристалының қабырғасына белгілі жылдамдықпен электрондар шоғы, «электрондық пушкадан» бағытталды. Коллектор электрондарды регистрация жасап отырды. Кристалды бастапқы шоқтың айналасында айналдырып отырдық. Электрондардың энергиясы 50эВ болды. Кристалл вакуумда орналасқан. Электрондардың сәулеленуінің интенсивтілігінің Ө-бұрышына тәуелділігі 540-та байқалды. Сол сияқты 44, 48, 64, 60В кезінде де максимумдар байқалды. Егер интенсивтіліктің Ө- бұрышына тәуелділігінің графигін қарастыратын болсақ, онда қисықтар дифракциялық қисықтарға сәйкес келеді. Демек, біз электрондардың дифракциясын бақыладық. Электрондар түскен жазықтықта никельдің атомдары кристалдың қабырғасында параметрі d болатын тор түзеді (3.7сурет).
3.7сурет. Тор
Эксперименттердің көрсетуі бойынша, егер
2
Егер k>1 (Дэвисон) болғанда да (3.2.1) өрнегі орынды болды. Дэвисон және Джермер, сол сияқты Томсон тәржибелері бойынша электрондар жұқа фольга арқылы өткенде дифракциялық сурет (құбылыс) пайда болады. Демек, материяның толқындары бар, толқын ұзындығы (электрондар және т.б бөлшектер үшін) де Броиль өрнегіндегі толқын ұзындығына сай келеді.
3.2 Қатты денелердің кристалл торлары Кристалл торы. Қатты денелердің ішкі құрылымын сипаттау үшін кеңістік немесе кристалл торы деген түсінікті енгізу ыңғайлы[12]. Кристалл торы кеңістік торын құрайды, тордың түйінінде бөлшектер (атом, молекула) орналасқан болады, сонымен қатты денені құрайды. 3.8 суретте қалың сызықпен ең кіші параллелепипед көрсетілген, бұл параллелепипедтің өзінің үш осі бойынша орын ауыстыруымен барлық кристалды құруға болады.
3.8 сурет. Кристалл торлары
Бұл параллелепипедті элементар немесе негізгі тор ұяшығы деп атайды. Бұл тор ұяшығын сипаттау үшін 6 шаманы беру керек: үш қырын (a,b,c) және осьтер арасындағы бұрыштарын (α,β,γ). Бұл шамаларды тор параметрлері деп атайды. Қарапайым тор түріне куб торы жатады, мұнда a=b=c және α=β=γ=900. Кейбір жағдайда тордың симметриясын нақты айқындау мақсатында элементар тор ұяшығын құрғанда олардағы бөлшектер тек тор шыңдарында ғана орналаспай, тағы тор ұяшығының басқа нүктелерінде де орналасқан болады. Мысалы, көлем центрленген торда кеңістік диагональдардың қиылысқан нүктесінде қосымша бір бөлшек орналасқан болады (3.9б сурет), жақ центрленген торларда жақ диагональдарының қиылысқан нүктелерінде қосымша бөлшектер орналасқан болады (3.9.в сурет), т.б. Енді түйіндерді, бағыттарды және тордың жазықтықтарын белгілеуді қарастырайық. Бұл белгілеулерді Миллер индекстері деп атайды.
3.9 сурет. Көлем центрленген торлар
3.10 сурет. Тордың координаталары
Бұл координаттарды мынадай түрде жазуға болады:
x=ma, y=nb, z=pc (3.13)
мұндағы a,b,c – тор параметрлері, m,n,p – бүтін сандар. Ось бойымен өлшенетін бірлікті метр деп есептемей, бірлік ретінде тордың a,b,c параметрлерін алсақ, онда тор координаталары m,n,p бүтін сандар болады. Бұл сандарды түйін индекстері деп атайды және былай жазылады: [[mnp]]. Теріс индекс болса, теріс таңба индекс төбесіне қойылады: [[ Бағыт индекстері.Кристалдағы бағытты сипаттау үшін координата басынан тура сызық алынады[18]. Ол сызықтың орналасуын бірінші түйіннің mnp индексі анықтайды, 3.10 суретте көрсетілгендей сызық сол бірінші түйіннен өтеді. Сондықтан түйіннің тор индекстері бағыт индексі де болады. Бағыт индексін [mnp]-мен белгілейді. Бағыт индексінің анықтамасы бойынша оны үш ең кіші бүтін сан анықтайды екен, бұл сандар осы бағыттағы ең жақын түйіннің орналасуын анықтайды. Мысалы, координата басынан және [[435]] түйіннен өтетін бағыт индексі [435] болады. Мысал ретінде куб торының негізгі бағыттарын көрсетуге болады, 1.9 суретте көрсетілген. Тор осьтерінің индекстері: ОХ осінің индексі [100], ОУ осінің - [010], ОZ осінің - [001]. Жақ диагональдарының индексі: bc жағы диагоналының индексі [011], ас жағы диагоналының - [101], ав жағы диагоналының - [110], кеңістік диагоналының индексі - [111]. Кристалл жақтарының индекстері[12].Кристалл жақтарының орнын кристалл торының осьтерін қиып өтетін A,B,C кескіндер айқындайды. Мұндай жазық теңдеуінің түрі мынадай болады:
3.11 сурет. Куб торының бағыттары
Мұндағы X,Y,Z – осы жазықта жататын нүктенің координаталары. Егер кристалл жазығы(жағы) тор түйінінен өтетін болса (тек сондай жақтар қарастырылады), онда жазықта жататын кез келген түйіннің координаталары түйін индекстеріне тең: x=m, y=n, z=p Сондықтан жазық теңдеуін мынадай түрде жазамыз:
m,n,p бүтін сан болғандықтан, (1.12) теңдеу 1/А, 1/В, 1/С қатынастар рационалды сандар болуы керек, олардың қатынастарын h,k,l үш бүтін сан қатынастарымен ауыстыруға болады:
Осы h,k,l сандар кристалл жазықтарының индекстерін береді, олар былай белгіленеді: (hkl). Жазық индекстерін былай анықтайды: тор осьтеріндегі жазықты қиып өтетін ось бірлігімен алынған А,В,С кескіндерді сол кескіндердің кері мәндеріне сәйкес, яғни 1/А, 1/В, 1/С етіп жазады. Алынған 1/А, 1/В, 1/С бөлшектерге ортақ бөлім табады. Ортақ бөлім Д болсын дейік, онда бірінші бөлшекке Д/А, екіншіге Д/В, үшіншіге Д/С болады. Д/А, Д/В, Д/С бүтін сандар кристалл жазығының h,k,l индекстері болады, яғни
Мысалы: 1. Тор осьтерін қиып өтетін А=1, B=2, C=3 кескіндерге сәйкес кристалл жазықтығының индексін анықтайық. Шешім: 2. Тор осьтерін қиып өтетін A=1/2, B=2, C=1/3 кескіндерге сәйкес кристалл жазығының индексін анықтайық. Шешім:
(1.14) қатынастан тор осінен өтетін жазықтықты қиып өтетін кескінді сол жазықтықтың индексімен анықтауға болатыны көрініп тұр, яғни
Сондықтан жазық индексі (hkl) арқылы тор осьтерін қиып өтетін кескіндерді анықтау үшін индекстердің кері мәнін жазып, яғни 1/h, 1/k, 1/l, олардың ортақ бөлімін (Д) анықтайды. Онда (1.15) теңдеулер арқылы кескіндер анықталады: А=Д/h, В=Д/k С=Д/l 3. Тор осіндегі (123) жазықты қиып өтетін кескіндерді анықтайық. Мысал ретінде 3.12 суретте көрсетілгендей куб торларының негізгі жақтарының индекстерін анықтайық[18].
3.12 сурет. Куб торы жақтарының индекстері
Куб жақтарының индекстері: «с» жақтың индексі – (001), «а» жақтың индексі – (100), «в» жақтың индексі – (010). Жақтың диагоналынан өтетін жақтың индексі (ромбалық додекаедр жағының индекстері: (110), (101), (011), т.б. осьтерді бірлік қимамен қиып өтетін жазықтардың (октаэдр жазықтарының) индекстері:
3.13 сурет. Гексагональды кристалдардың жазықтары
Қатты денелердегі анизотропия. Моно және поликристалды қатты денелер. Қатты денелердің бөлшектері кристал торында біртекті қатар-қатар орналасқан деп есептейік (кристалдардағы ақауларды ескермейміз). Әрбір бағыттағы қатты денелердің қасиеттерін бөлшектердің сол бағытта қаншалықты тығыз орналасуы анықтайтын болғандықтан, алынған бағыт бойынша қатты денелердің қасиеттері әр түрлі болуы керек. Дене қасиетінің бағытқа тәуелділігін (қасиеттің бағыттылығын) анизотропия деп атайды. Арнайы жағдайда қатты денелерді бір кристалл түрінде өсіруге болады, яғни монокристалл түрінде. Бірақ көп жағдайда ерітінділерде (балқыған денелерде) бір мезгілде көптеген кристаллизацияланатын орталықтар пайда болып, көптеген өзінше бөлек кристалдар болуына алып келеді. Бұл кристалдардың өсуінің арқасында олар бір-біріне жақындай түседі. Сонымен көптеген бөлшектер пайда болады, яғни поликристалл. Өскен кристалиттер (дәндер) әр түрлі формада болады, сыртқы көрінісі ішкі ретті құрамына сәйкес келмейді. Себебі олардың (дәндердің) орналасуы суытылған ерітіндіде (сұйық күйдегі затта) кристаллизация орталығы кездейсоқ орналасқан болады. Сондықтан кристалдарда олардың қасиеттері кристалл бағытына елеулі тәуелді болуы байқалмайды, яғни олар изотропты болады. Сонымен қатар өскен дәндердің әртүрлі бағытта болғандығы дәндер (кристаллиттер) шекарасында кристаллиттер шекарасы деп аталатын әртүрлі қалыңдыққа ие қабаттар пайда болады. Бұл дән шекаралары поликристалл агрегатының механикалық қасиетінің қалыптасуына елеулі әсер етеді. Өте таза, қоспа атомдардың болуы жоқтың қасы болғанда да дәнаралық қабатындағы тор дән торына қарағанда елеулі ауытқыған болады. Бұл тор ауытқуы бір атом аралығымен шектелмейді, бірнеше атом аралықтарына дейін орын алады. Бұл торлары ауытқыған атомдармен дән шекарасындағы атомдар бір-бірімен әсерлеседі. Дән шекарасындағы ретсіздік дәрежесі үлкен (жоғары) болған сайын, ретсіздік көлемі (ретсіздік қабыршақтың қалыңдығы – ені) үлкен (кең) болады және олардың тор ауытқулары ұлғаяды, яғни тор аууытқу дәрежесі өседі. Кристаллит тор жолағындағы ауытқулар бұл жолақта артық еркін энергияның шоғырлануына (локализация) алып келеді. Еркін энергияның шоғырлану бірнеше тәжірибелерде дәлелденген, Мысалы, Галмерс өте таза қалайының (олово) дән шекаралары дәннің балқу температурасынан төмен температурада балқығанын анықтаған. Дән шекарасы бойынша өтетін диффузия жылдамдығы, көлем бойынша өтетін диффузия жылдамдығынан жоғары. Рекристаллизация кезіндегі жаңа дән өсуі ескі дән шекарасында басталады немесе интенсивті пластикалық деформация өткен кезде басталады, ал рекеристаллизация ескі кристалл торларын өзгертеді. Егер металда қоспа атомдар болса, онда кристаллизация кезінде қоспа атомдар дән шекараларына орналасады, соның арқасында кристаллиттер (дәндер) аралығында құрамдары да, қасиеттері де дәндерге қарағанда өзгеше жолақтар пайда болады[18]. Химиялық элементтердің кристалдық құрылымдары. Қатты күйдегі химиялық элементтер ішкі ретті құрылымды кристалдық денелерді құрайды. Кристалл құрылымының түрін негізінен құрылым бөлшектердің (атомдар, иондар, молекулалар) арасындағы байланыс күшінің түрі (характері) анықтайды. Бұл бөлшектер арасында 4 негізгі байланыс болғандықтан 4 типті кристалл торын құрайды: ионды немесе координационды тор, бұл торда атомдар арасындағы негізгі байланыс ионды болады; поляризационды немесе молекулярлы тор; мұндағы молекулалар арасындағы байланыс Ван-дер-Ваальс күштері арқылы болады; валентті байланысты атомдық тор және металды байланысты металл торлары болады. Таза бір күш түрімен байлансқан, яғни өзара әсерлесетін атомдарды сирек кездестіретін секілді, құрылыма түрінде де таза бір типті тордың кездесуі де өте сирек. Көп жағдайда тор өткінші (переходной) болып келеді, яғни тордың өткінші болуы атомдар арасындағы байланыстың түрі екі немесе бірнеше болудың арқасында химиялық элементтердің кристалдық құрылымын жобамен 4 класқа бөлуге болады, 1.3 кестеде берілгендей.
3.1 кесте Химиялық элементтердің кристалдық құрылымы
Бұл құрылмдарды талдаудың IV кластан бастаған ыңғайлы. Бұл класқа инерт газдардың құрылымы жатады. Инерт газдардың сұйық күйге және кристалға айналғанда электрондары симметриялы сфералық қабаршақтары бар атомдар арасындағы байланыс әлсіз Ван-дер-Ваальс күштің пайда болуынан болады. Бұл күштің әсерінен симметриялық атомдар тығыз орналасқан жақ центрленген куб торын құрайды, 1.7 суретте көрсетіліп кеткен. Тордағы әрбір атомды оған жақын орналасқан 12 атом қоршайды. Атомға жақын орналасқан атомдардың санын тордың координациялық саны деп атайды. ІІІ класс. Бұл класқа қысқа периодтан кремний және көміртегі IVB топтан германий және қалайы және VВ, VIB және VIIB топтарындағы барлық элементтер жатады. Бұл кластағы барлық элементтер 8-N дәрежесіне сәйкес кристаллизацияланады, яғни тордағы әрбір атом 8-N жақын атомдармен шоғырланған, мұндағы N-сол элемен орналасқан топтың номерін білдіреді. Мысалы, алмаз, кремний, германий және сұр қалайы N топтың элементтеріне жатады. Сондықтан олардың торының координациялық саны 8-4=4 болады. Шынында да, бұл элементтердің барлығы тетраэдралық торға ие, мұнда әрбір атом 4 жақын атомдармен қоршалған, 1.12(а) суретте көрсетілгендей[18].
3.14 сурет. Тетраэдралық торлар
Мышьяк, фосфор, сурьма және висмут периодтық жүйенің V тобында орналасқан, торларының координациялық саны 8-5=3 тең. Бұларда әрбір атом бір жазықта 3 жақын атомдармен қоршалған, 1.12(б) суретте көрсетілгендей. Торлары жұқа қабыршақтардан тұрады. Атом қабыршақтары бір-бірімен Ван-дер-Ваальс күші арқылы байланысқан. Селен және теллур VI топта орналасқан, торларының координациялық саны 2-ге тең. Олардың атомдары ұзын спираль тізбектерден тұрады. Тізбектегі әрбір атомды жақын екі атом қоршайды, 1.12(в) суретте көрсетілгендей. Тізбектер өзара Ван-дер-Ваальс күштерімен байланысқан. Ал иод VII топқа жатады. Иодтың торында қос атомдар орналасады, 1.12(г) суретте көрсетілгендей. Бұл қосақталған атомдар бір-бірімен Ван-дер-Ваальс күштерімен байланысқан болады. Сондықтан да иодтың тез буланып ұшып кетуіне алып келеді. 8-N ережесі арқылы химиялық элементтердің кристаллизациялануын оңай түсінуге болады. Мысалы IV топтағы элемент атомының сыртқы қабыршағында 4 электрон орналасқан. Тұрақты 8 электронды конфигурацияны құрастыру үшін тағы 4 электрон жетіспейді. Бұл кемшілікті толтыру үшін жақын орналасқан 4 атомдардың электрондарымен өзара алмасады, 1.12(а) суретте көрсетілгендей. Сондықтан да кристалл торындағы әрбір атом 4 жақын атомдармен қоршалған. Осы сияқты 8 электронға дейін сыртқы атом қабыршақтары Менделеевтің периодтық кестесіндегі V,VI,VII топтардағы элементтердің атомдары толтырылады[18]. І класс. Бұл класқа көп элементтер жатады, олар – металдар. Металл торларында атомдар емес, олардың иондары орналасқан. Олар инертті газдар секілді сфералық симметрияға ие. Сондықтан металдар кристаллизация кезінде инертті газдар секілді тығыз орналасқан торға ие деп күтуге болады. Шынында да, металдар 3 түрлі кристалл торларына ие. Координациялық саны 12-ге тең жақ центрленген куб (1.7(в) сурет), координациялық саны 12-ге тең гексагональды тығыз орналасқан тор (1.11 сурет) және 8 координациялық санға тең көлем центрленген куб (1.7(б) сурет). Бұл ең ұлпа торлы металл (кеңістікті атомдармен толтыру мағынасында). Идеал гексагональды торда ІІ класс. Бұл кластағы химиялық элементтер металл мен ІІІ кластағы 8-N ережемен кристаллизацияланатын элементтер арасындағы аралық кристалдарға жатады. ІІВ топтағы Zn, Cd, Hg металдар, олай болса олар жоғары координациялық санға ие металл торларының біріне жатуы керек. Ал шындығында Zn және Cd кристаллизацияланғанда ерекше гексагональды компакты құрылымға ие болады. с/а=1,633 болмай, бұл қатынас 1,9 тең болады. Бұл кристалдардың координациялық саны 12-ге тең болмай, 6-ға тең, яғни 8-N ережеге сәйкес келеді. Бұл атомдар базис жазықтығында орналасқан болады. Ал сынапқа (Hg) 8-N ереже толығымен орындалады, ол қарапайым ромбоэдрикалық құрылымға ие, мұнда әрбір атом 6 жақын орналасқан атомдармен қоршалған, яғни координациялық сан 6-ға тең. Бор ІІІВ топқа жатады, оның торы деформацияланған, әрбір атомы 5 жақын атомдарменқоршалған тормен сипатталады, яғни тордағы атомдардың орналасуы 8-N ережеге сәйкес келеді. Ерекше топтарға алюминий, индий, талий және қорғасын элеменииердің торларын жатқызуға болады. Олардың барлығы металдың немесе аз шамаға деформацияланған металдың құрылымына ие, бірақ бұл элементтердің атомдары кристалдарда жарым-жартылай ионизацияланған болуы мүмкін. Себебі олардың атом арақашықтығы ол элементтердің алдындағы элементтер атомдарының арақашықтығынан үлкен болып келеді. Мысалы, алюминий торының параметрі a=4,04Å болса, оның алдындағы магнийдікі a=3,2 Å, индийдікі a=4,87 Å болса, оның алдындағы кадмийдікі a=2,97 Å, қорғасындікі a=4,94 Å, оның алдыңғы сынаптікі a=3,83 Å. Әртүрлі кристалл құрылымы болуының себебін түсіндіру мақсатында көптеген теориялық зерттеулер болған. Солардың ішінде ең қарапайым таза металға кванттық механика арқылы атомдардың әртүрлі орналасуына анықталған атомдар арасындағы әсерлесу энергиясына қарағанда, кристалл құрылымының тұрақтылығына жүйенің (кристалдың) энергиясы минимальды болуы сәйкес келуімен дәлелденген. Таза металдардың және интерметалды қосындылардың құрылымын түсіндіруде Юм-Розери өзінің ерекше ұсынысын жасаған. Юм-Розеридің гипотезасы электрондық концентрация түсінігіне негізделген. Тордың бір атомына келетін валенттік электрондардың санын электрондық концентрация деп атайды. Металл торының түйінінде орналасқан оң заряды бар иондардың электрон газдармен бірін-бірі тарту күшін тудыратын себебі, электрондық концентрациясы бірдей әртүрлі металдардың және қоспалардың байланыс күштері ұқсас болады және олардың кристалдық құрылымы бір типті болады. Эксперимент нәтижелері бұл Юм-Розери ұсынысының дұрыс екенін дәлелдейді[18]. Менделеевтің периодтық кестесіндегі бір топта орналасқан химиялық элементтердің валенттік электрондары бірдей және олар негізінен бір құрылымға сәйкес кристаллизацияланады (1.3 кесте). AgZn, Cu3Al, Cu3Sn және басқа көп интерметалды қосындылардың электрондық концентрациясы, жобамен 1,5 тең және олардың кристалдық құрылымы бірдей – көлем центрленген куб. AgCd3, CuZn3 т.б. интерметалды қосындылардың электрондық концентрациясы 1,75 тең, олар гексагональды тығыз орналасқан құрылымға ие, т.с.с. Бірақ электрондық концентрация ережесі барлық жағдайда орындала бермейді, кейбір кезде бір топта орналасқан элементтердің кристалдық торы әр түрлі болады. Сонымен қатар электрондық концекнтрациясы бірдей, бірақ кристалдың құрылымы әртүрлі көптеген қосындыларды көрсетуге болады. Бұл мәліметтерге қарағанда, кристал құрылымын тек электрондық концентрация анықтай алмайды, сонымен қатар құрылымға тор элементтері арасындағы өріс күші де (оның интенсивтілігі, геометриясы), т.б. факторлар да өзінің әсерін тигізеді.
Рентгендік аппараттар
Зерттелуші объектілерден рентгеннограммалар есептегіштер көмегімен (ионизациялық тіркеу) және ақпараттарды диаграммалық лентаға шығарумен (ДРОН-2; ДРОН-3 және т.б. ортақ мәндегі рентгендік дифрактометрлер) дифракциялық көріністерді тіркеуші және фотографиялық тіркеуші (УРС-26; УРС-60 және т.б.) рентгендік қондырғыларда алынуы мүмкін. Егер зерттелетін объект ұнтақ түрінде болса, онда дифракциялық көріністі алу үшін фотометод қондырғысын да, дифрактометрді де пайдалануға болады. Егер үлгі жазық үлгі немесе шлиф түрінде болса, онда дифрактометрді пайдалану керек. Дифрактометрлерді пайдалану зерттеу ұзақтығын қысқартады, өлшеу дәлдігі мен сезімталдығын жоғарылатып, пленканың фотографиялық және денситометрлік өңделуін шектеуге мүмкіндік береді. Дегенмен қарқындылығы өте кіші сызықтарды фотографиялық тіркеу кезінде спектрді визуалды түрде ұтымды пайдалануға болады. Есептегіш әрбір уақыт сәтіндегі аз бұрыштық интервалда дифракция қарқындылығын тіркейді. Дифракциялық көрініс фотометрдегідей бірмезгілде емес, біртіндеп тіркеледі. Сондықтан біріншілік шоқ қарқындылығы уақытпен тұрақты болуы, ал түсірілім сызбасы – тіркеудің әрбір нүктесінде қарқындылыұты ұлғайту үшін фокустеуші болуы тиіс[4].
4.1 Рентген құрылғысы және тәжірибелік әдістер
Брэгг-Вульф (1.4) тендеуінен дифракциялық максимумды байқау үшін θ мен Рентгенді сәулелену көзі ретінде екі электродты электро-вакуумды құрылғылы рентген түтігі қолданылады. Онда рентгенді сәулені қоздыру үшін зат пен жылдам электрондар өзара әсерлесуін туғызатын, металды нысанаға қарай бағытталған кинетикалық энергиясы жоғары бос электрондар ағынын жасайды және рентгенді сәулелену пайда болады. Рентгенді түтік тұтастай шыныдан немесе шыны мен металдан жасалған баллон тәріздес болып келеді (1.6 сурет). Баллонда катод пен анод орналасқан. Катод ретінде 2273-2973 К-ге дейін төменгі вольтты трансформатормен қыздырылған вольфрамнан жасалған V-тәрізді немесе шиыршықты (спиралды) жіпшелер атқарады. Катодты электрондар ағынын анодқа жинақтайтын құрылғыда орналастырады. Анод ретінде массивті мыс цилиндрінің ішкі түп жағындағы жалпақ (тегіс) бөлігі атқарады. Электрондарды соққылауда нысана ролін атқаратын бұл бөлікке қажетті характеристикалық сәулелену толқын ұзындығын алуға арналған сол немесе басқа металдан жасалған қабатты (дәнекерлеу немесе гальваникалық әдіспен) қондырады[8]. КПД түтігі төмен (~1-3%) болғандықтан, онымен жұмыс істеу кезінде барлық қажетті қуат жылуға айналады, ал жылуды шығару үшін анодты сумен салқындату жүйесін қолданады. Жұқа бериллий фолгасының терезесі 0,4нм және одан кіші сәулелерді өткізуге мүмкіндік береді. Мұндай типті түтікпен жұмыс істеу үшін оны 1-ден 10-2 Па шегінде сирету керек. Рентгенді сәулеленуді қолдану диапазонының кендігіне қарай рентген түтіктердің әртүрлі варианттары бар екендігін де айта кеткен жөн.
1 - анодты сумен салқындату; 2 - рентген сәулесінің шоғыры; 3- шығару терезесі; 4- кақпакша; 5 - катод; 6- түтік корпусының шыны бөлігі; 7- вольфрамды катодының кыздыру трансформаторы; 8 - жоғары тұракты ток тізбегі; 9 - электрондар ағыны; 10- анод; 11- массивті мыс цилиндрі 4.1 сурет. Құрылыстық талдауға рентгенді түтіктің сызбасы
Қазіргі кездегі құрылысты зерттеулерді әртүрлі модификациялы үш негізгі әдіс қолданылады. Лауэ әдісімонокристалдар құрылысын зерттеуде қолданылады. Мөлшері 1мм-ден аспайтын монокристалды үлгі жалпақ спектр беретін рентген сәулесінің тар шоғыры жолына орналастырады (1.7 сурет (а)). Бұл шоғырда сәулелену сол немесе басқа толқын ұзындықтары үшін (4) жағдайын қанағаттандыратын толқын ұзындығының кең диапа-зонын қамтиды және дифракциялық рефлекс пайда болуына әкеледі. Шындығында, кристалл дифракциялық шағылулардың дискреттік жиынын таңдап алады. Жазық пластинкадағы (фотопленкадағы) дифракция нәтижесінде эллипс, гипербола түзу сызық түрінде орналасқан қара «дақтар» пайда болады және біріншілік шоғырдан дақ арқылы өткен (штрихталмаған шеңбер) жағдайда Брэгг-Вульф теңдеуі орындалады (1.7-сурет (а)). Монокристалдардың белгілі бір бағытталуда алынған картинасы (лауэграмма) ориентациясы мен кристалл симметриясының негізгі элементтерін тұрақтандырады, бірақ ол құрылыстық характеристикаларын (кристалдардың элементарлы ұяшықтарының размері, ондағы атомдар саны және т.с.с.) бере алмайды. Егер кристалл, мысалы, 4-ші ретті симметрия осінде түскен шоғырларға параллелді орналасқан болса, онда лауэграмма да 4-ретті симметрия осін иемденеді[4]. Егер кристалл құрылысы алдын-ала белгілі болмаса, онда дифракциялық дақтар жиынтықтарын ашып көрсету қиындықтар туғызады. Негізінен бұл әдіс симметриясын тез анықтау үшін немесе құрылысы белгілі кристалдың ориентациясы үшін қолданылады. Лауэ әдісі, сонымен қатар, кристалды механикалық және термиялық өндеу кезінде пайда болатын бүлінулер мен ақаулардың размерлерін анықтау үшін де қолданылады.
1-жалпақ спектрлі рентгенді сәуленің шыққан шоғыры; 2-корллиматлор; 3-монокристалды үлгі; 4-шашыраған сәуле; 5-жазық фотопленка
4.2 сурет.Лауэ әдісімен жұмыс істейтін қрылғы сызбанұсқасы (а), және дифракциялық кескіні (лауэграмма) (б)
Кристалдардың құрылысы туралы толығырақ ақпаратты кристалды айналдыру әдісін қолдану арқылы алуға болады. Бүл әдістің мәнісі мынада: монохроматты рентгендік сәуле жолында орналастырылған монокристалл кристалдағы маңызды кристаллографиялық бағыттардың біріне сәйкес келетіндей етіп ось бойымен біркелкі айналдырылады және ол сәуле бағытына перпендикулярлы болып келеді (4.2 сурет (а)). Шоғыр көзінен түсетін монохроматизация кристалл-монохроматормен немесе фильтр көмегімен жүргізіледі. Коллиматор арқылы өткен монохроматталған шоғыр үлгінің айналу кезіндегі бұрыш мәні θ (1.4) жағдайын қанағаттандыратын әрбір рет монокристалды үлгінің белгілі атомдык жазықтығында дифракцияланады. Вертикальды айналу осіне параллелді жазықты |
 ,
,  3,4,5,... (3.1)
3,4,5,... (3.1)


 ), (3.1сурет).
), (3.1сурет).
 R(
R(  ), n=2,3,4,...
), n=2,3,4,... R(
R(  ), n=4,5,6,...
), n=4,5,6,... R (
R (  ), n=5,6,7,...
), n=5,6,7,...  R(
R(  ), n=6,7,8,...
), n=6,7,8,... R(
R(  ) (3.2)
) (3.2) ;
; 

 ) мен Т(
) мен Т(  ) функциялары спектрлік термдер немесе термдер деп аталады. Әрбір серияда Т(
) функциялары спектрлік термдер немесе термдер деп аталады. Әрбір серияда Т(  ) тұрақты болады да Т(
) тұрақты болады да Т(  ) өзгеріп отырады.
) өзгеріп отырады. ,
,  + және т.с.с.
+ және т.с.с. стационар күйден энергиясы аз
стационар күйден энергиясы аз  стационар күйге өткенде сәуле (фотон) шығарады. Шығарылған фотонның энергиясы стационар күйлердің энергиясының айырмасына тең:
стационар күйге өткенде сәуле (фотон) шығарады. Шығарылған фотонның энергиясы стационар күйлердің энергиясының айырмасына тең:  (3.3)
(3.3)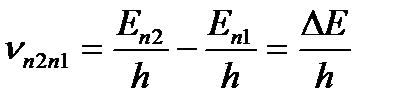 (3.4)
(3.4) (3.5)
(3.5) 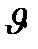 -электронның жылдамдығы;
-электронның жылдамдығы; - келтірілген Планк тұрақтысы.
- келтірілген Планк тұрақтысы.
 Ф/м-электр тұрақтысы,
Ф/м-электр тұрақтысы, -бұрыштық жылдамдық, бұдан
-бұрыштық жылдамдық, бұдан (3.7)
(3.7) соңғы екі формуладан
соңғы екі формуладан  -орбитадағы қозғалатын электронның орбитасының радиусы:
-орбитадағы қозғалатын электронның орбитасының радиусы:

 болғанда (сутегі үшін
болғанда (сутегі үшін  ).
).

 .
. -сутегі атомындағы элкронның бірінші орбитасының радиусы - Бор радиусы деп аталады.
-сутегі атомындағы элкронның бірінші орбитасының радиусы - Бор радиусы деп аталады.
 және
және  кезінде орбиталар мен энерия мәндерінің айырмашылықтары өте зор. Бірақ та,
кезінде орбиталар мен энерия мәндерінің айырмашылықтары өте зор. Бірақ та,  және
және  мәндері үшін орбита мөлшерінің де, энергиялардың да айырмашылықтары жоққа тән (2.6.1-сурет).
мәндері үшін орбита мөлшерінің де, энергиялардың да айырмашылықтары жоққа тән (2.6.1-сурет).

 ( кейде оны азимутальдық дейді)
( кейде оны азимутальдық дейді)  -электронның импульс моментімен байланысты. Ол о-ден n-1-ге дейінгі бүтін мәндерді қабылдайды. Импульс моментінің р шамасы
-электронның импульс моментімен байланысты. Ол о-ден n-1-ге дейінгі бүтін мәндерді қабылдайды. Импульс моментінің р шамасы  (3.9)
(3.9) (3.10)
(3.10)
 . Егер атомға сыртқы магнит өрісі
. Егер атомға сыртқы магнит өрісі  әсер етсе, онда импульс моментінің сол өріс бағытына түсірілген прсекциясы
әсер етсе, онда импульс моментінің сол өріс бағытына түсірілген прсекциясы  - ге еселес болады, яғни
- ге еселес болады, яғни (3.11)
(3.11)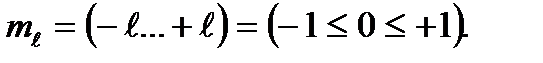
 -дің
-дің  мәндері болады.
мәндері болады.


 және электрондардың энергиясы 54эВ болғанда, интенсивтіліктің максимумдары θ=50
және электрондардың энергиясы 54эВ болғанда, интенсивтіліктің максимумдары θ=50 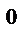 -та байқалады; бұл 1,65
-та байқалады; бұл 1,65  болатын толқын ұзындығына сәйкес келеді, егер k=1 болғанда; Вульф-Брегг өрнегі:
болатын толқын ұзындығына сәйкес келеді, егер k=1 болғанда; Вульф-Брегг өрнегі: (3.12)
(3.12)


 ]].
]]. (3.14)
(3.14)
 (3.15)
(3.15) (3.16)
(3.16)

 (3.17)
(3.17) - рационал сандар, онда жалпы бөлгіш 6 болады. Олай болса, 6/1=6, 6/2=3, 6/3=2, яғни h=6, k=3, l=2, жазық индексі (632) болады екен.
- рационал сандар, онда жалпы бөлгіш 6 болады. Олай болса, 6/1=6, 6/2=3, 6/3=2, яғни h=6, k=3, l=2, жазық индексі (632) болады екен. - рационалды сандар. Ортақ бөлім 2 болады, онда
- рационалды сандар. Ортақ бөлім 2 болады, онда  ,
,  ,
,  , жазық индексі (416).
, жазық индексі (416). ,
,  ,
, 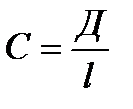 (3.18)
(3.18)
 ,
,  ,
,  ,
,  т.б. гексагональды кристалдардың жазықтарын белгілеу үшін 4 негізгі координата жүйесі қолданылады, 1.11 суретте көрсетілген: үш (а1,а2,а3) бір-біріне 1200 жасаған ось, бұл осьтер алты жақты призманың бетінде жатады (базис жазықтығы), ал төртінші ось (с) базис жазықтығына перпендикуляр. Әрбір жазық 4 индекспен белгіленеді: hkil. Қосымша индекс і үшінші орынға қойылады, бұл индекстің мәні h және k индекстер арқылы есептеледі: i=-(h+k). а1, а2, а3 осьтеріне параллель базис жазығының индексі (0001) болады. Призма бүйірінің жағына параллель жазықтың индексі мынадай типті болады:
т.б. гексагональды кристалдардың жазықтарын белгілеу үшін 4 негізгі координата жүйесі қолданылады, 1.11 суретте көрсетілген: үш (а1,а2,а3) бір-біріне 1200 жасаған ось, бұл осьтер алты жақты призманың бетінде жатады (базис жазықтығы), ал төртінші ось (с) базис жазықтығына перпендикуляр. Әрбір жазық 4 индекспен белгіленеді: hkil. Қосымша индекс і үшінші орынға қойылады, бұл индекстің мәні h және k индекстер арқылы есептеледі: i=-(h+k). а1, а2, а3 осьтеріне параллель базис жазығының индексі (0001) болады. Призма бүйірінің жағына параллель жазықтың индексі мынадай типті болады:  . Мұндай бір-біріне параллель емес беттер (жазықтар) үшеу; оларды бірінші типтегі (жазықтар) беттер деп атайды.
. Мұндай бір-біріне параллель емес беттер (жазықтар) үшеу; оларды бірінші типтегі (жазықтар) беттер деп атайды.

 тең.
тең. арасында белгілі бір байланыс қажет екенін қөруге болады. (1.4) жағдайы екі әдіспен орындалуы мүмкін: қажет толқын үзындығын немесе сәуленің түсу бұрышын таңдау. Егер монохроматты (
арасында белгілі бір байланыс қажет екенін қөруге болады. (1.4) жағдайы екі әдіспен орындалуы мүмкін: қажет толқын үзындығын немесе сәуленің түсу бұрышын таңдау. Егер монохроматты ( 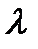 =const) рентгенді сәуле жолына орналасқан зерттелетін кристалды сәуле осіне перпендикулярлы бұрып, шағылысатын жағдайға кристалдың жазық жүйесін кезекпе-кезек қоятын болсақ, онда шашыраудың толық кескіні байқалады. Дифракциялық кескінді рентгенді сәулеленудің үздіксіз спектрін беретін көзді қолдана отырып үлгіні айналдырмай-ақ алуға болады. Бұл жағдайда үздіксіз спектрде кристалдың барлық жазықтық жүйелері үшін міндетті түрде (1.4) тендеуін қанағаттандыратын толқын ұзындықтары
=const) рентгенді сәуле жолына орналасқан зерттелетін кристалды сәуле осіне перпендикулярлы бұрып, шағылысатын жағдайға кристалдың жазық жүйесін кезекпе-кезек қоятын болсақ, онда шашыраудың толық кескіні байқалады. Дифракциялық кескінді рентгенді сәулеленудің үздіксіз спектрін беретін көзді қолдана отырып үлгіні айналдырмай-ақ алуға болады. Бұл жағдайда үздіксіз спектрде кристалдың барлық жазықтық жүйелері үшін міндетті түрде (1.4) тендеуін қанағаттандыратын толқын ұзындықтары 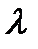 табылады.
табылады.
