 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Раздел 2. Метод Мак-Кормака 12
Метод Мак-Кормака – это конечно-разностный метод типа предиктор-корректор. Метод Мак-Кормака широко используется для решения задач движения сжимаемого потока и других задач последние 30 лет. С момента появления схема Ма-Кормака претерпела множество модификаций и обобщений. Существуют как явная, так и неявная версии этого алгоритма. Также развита модификация для применения в методе конечных объемов. Метод Мак-Кормака считается краеугольным камнем вычислительной гидродинамики. Как явная, так и неявная версии метода позволяют решать гиперболические и параболические уравнения для положительного временного шага, при этом проявляя хорошие диссипативные и дисперсионные краевые свойства. Популярность явного метода Мак-Кормака обусловлена как простотой его выражений, так и простотой применения этого метода, в том числе и для многомерных задач. Этапы предиктора и корректора используют прямое дифференцирование для производных по времени первого порядка, и одностороннее дифференцирование пространственной производной первого порядка. (Bernard., 1992) Для предиктора и корректора при дифференцировании по времени используется только разности «вперед». А вот направления пространственного дифференцирования в предикторе и корректоре всегда противоположны. В примере, если в схеме на шаге предиктор используются разности «назад», то в корректоре – «вперед». Разности «назад» и «вперед» можно циклически чередовать: таким образом, устраняется рассогласование, обусловленное аппроксимацией односторонними разностями, благодаря чему при вычислении нет нужды в расчете Якобиана, как это происходит в одно-шаговой явной схеме типа Лакса-Вендроффа Основой метода Лакса-Вендроффа является разложение в ряд Тейлора до слагаемого второго порядка, где Мак-Кормак предложил альтернативных подход к оцениванию Т.е.
Решив уравнение для
В итоге получим
Используя свойства частных дифференциальных уравнений, проведем замену
Заменяя Рис.2.1. Прямоугольная расчетная сетка Такая замена приводит к неявному функциональному дифференциальному уравнению, которое крайне сложно решить в рамках нелинейных частных дифференциальных уравнений. Мак-Кормак предложил процедуру предиктор-корректор, которая расчитывает спрогнозированные величины
где
Проведя некоторые преобразования, получим формулу более пригодную для компьютерного расчета:
Уравнения описывают приближение методом Мак-Кормака для линейного конвективного уравнения. Шаблон аппроксимация представлен на рис.2.2. Рис.2.2. Шаблон метода Мак-Кормака
Метод Мак-Кормака использует аппроксимацию разностями «вперед» для Метод Мак-Кормака при первом рассмотрении кажется ничем иным, как одно-шаговым методом Лакса-Вендроффа. Однако они идентичны только для линейных конвективных уравнений. Для нелинейных частных дифференциальных уравнений и систем нелинейных частных дифференциальных уравнений эти два метода похоже ведут себя, но дают не идентичные решения. При этом для двух- и трехмерных пространств метод Мак-Кормака более эффективен, чем метод Лакса-Вендрофа. Так как для линейных конвективных уравнений метод Мак-Кормака идентичен методу Лакса-Вендроффа, то и анализы устойчивости и точности решению дают сходные с методом Лакса-Вендроффа результаты. Таким образом, метод дают решение с порядком точности Для равномерных сеток схема Лакса-Вендроффа, а значит и схема Мак-Кормака имеет второй порядок аппроксимации по времени и пространству на гладких решениях. При сквозном счете скачков (разрывных решений) она дает заброс и затухающие колебания решения за фронтом движущегося разрыва, то есть является немонотонной. Контактные разрывы эта схема размазывает только за счет физической вязкости, что является ее достоинством. Немонотонность схемы Лакса-Вендроффа для задач упругопластического деформирования приводит к дополнительным ошибкам в расчете истории напряженно-деформированного состояния из-за нефизических смен режимов нагружение-разгрузка за ударными волнами. Поэтому для исключения таких ошибок ее используют совместно с какими-либо процедурами дополнительной монотонизации решений, которые рассматриваются далее. Подчеркнем также необходимость обеспечения консервативности для сходимости результатов сквозного счета разрывных решений. В отличие от схемы Лакса Вендроффа вместо осреднения Лакса на предикторе и центральных разностей здесь для стабилизации применены односторонние разности и на предикторе, и на корректоре, но в разные стороны. То есть на одном из таких полушагов схема заведомо неустойчива, а на другом – наоборот обладает избыточным запасом устойчивости. В сумме двух шагов получается устойчивая для линейных уравнений схема второго порядка точности. Как и в схеме Лакса-Вендроффа диффузионный оператор учитывается только на корректоре по обычной центрально-разностной схеме. Следует отметить, что в нелинейных задачах газовой динамики схема Мак-Кормака локально неустойчива в сверхзвуковых зонах разрежения и в дозвуковых зонах возвратно-циркуляционного течения. Как и схема Лакса-Вендроффа схема Мак-Кормака немонотонна. Введением монотонизаторов ее можно заставить работать устойчиво. Отметим, что эквивалентная по дифференциальным приближениям схема с центрально-разностной аппроксимацией содержит дополнительную искусственную вязкость на предикторе и корректоре с альтернирующим по знаку коэффициентом искусственной вязкости ± | U | / 2 h . Это означает, что на одном из шагов вводится дополнительная диффузия, а на другом – антидиффузия.
Выводы Метод Мак-Кормака дает исследователям в области гидродинамики очень удобный инструментарий для решения уравнений движения сжимаемой и несжимаемой жидкости, в том числе для решения уравнений Ейлера и Навье-Стокса. Простота применения метода Мак-Кормака, высокая эффективность и точность решения являются очень важными свойствами данного численного метода. Благодаря применению процедуры предиктор-корректор метод становится легко применяемым для компьютерного расчета, даже при обобщении одномерной задачи на двумерный и трехмерный случаи. Метод Мак-Кормака также является хорошей, твердой базой для создания численных модификаций четвертого порядка точности и выше. Метод Мак-Кормака также проявляет высокие свойства стабильности. В этом отношении метод Мак-Кормака повторяет метод Лакса-Вендроффа и дает те же условия устойчивости. Для одномерного случая, параметром устойчивости выступает число Куранта и связанные с ним величины.
Список использованной литературы 1. Bernard Robert. – A MacCormack scheme for incompressible flow. – Computers Math. Applic. Vol.24. No. 5/6. 1992 – pp. 151 – 168. 2. Caughey, Hafez. Contributions of Robert Mac-Cormack to Computational Fluid Dynamics, in: Frontiers of Computational Fluid Dynamics 2002, Caughey, Hafez (ed); p.1-26, London, World Scientific Publishing Co, 2002. 3. Gottlieb David. Dissipative Two-Four Methods for Time-Dependent Problems. – Mathematics of computation, Vol.30, No. 136, 1976. – pp. 703-723 4. Griffiths Davis, Higham Desmond. MacCormack’s method for Advection-Reaction Equations. – University of Strathclyde Mathematics Research Report, No.25. 1999. 5. Griffiths Davis, Higham Desmond. Runge Kutta and MacCormack’s dynamics. – University of Strathclyde Mathematics Research Report, No.18. 1999. 6. Hoffman J. D. Numerical methods for engineers and scientists. Second edition revised and expanded. – New York: Marcel Dekker, Inc. – 2001. – pp. 651 – 701. 7. Anderson J. D. Journal of Computational fluid dynamics: the basics with application. / McGraw-Hill Series in Mechanical Engineering. – New York: McGraw-Hill, Inc. – 1995. – pp. 216 – 280. 8. Kurganov A. Tadmor E. New High-Resolution Central Schemes for Nonlinear Conservation Laws and Convection–Diffusion Equations. – Journal of Computational Physics 160, 2000. – 241–282 p. 9. Bram V. Upwind and High-Resolution Methods for Compressible Flow: From Donor Cell to Residual-Distribution Schemes. - Communications in computational physics. Vol. 1, No. 2, 2006. – pp. 192-206. 10. MacCormack R.W. Numerical Solution of the Interaction of a Shock Wave with a Laminar Boundary Layer, in: Proceedings of the Second International Conference on Numerical Methods in Fluid Dynamics, Lecture Notes in Physics, Holt M. (ed.) vol. 8, p.151-163, New York, Springer-Verlag, 1971. 11. MacCormack R.W. Viscosity Effects in Hypervelocity Impact Cavering, in: Frontiers of Computational Fluid Dynamics 2002, Caughey, Hafez (ed); p.1-26, London, World Scientific Publishing Co, 2002. 12. Wendroff Burton. The stability of MacCormack’s method for the Scalar Advection Equation. – Appl. Math. Lett., Vol.4., No. 2, 1992 – pp. 89-91. 13. Zalesak Steven. Fully Multidimensional Flux-Corrected Transport Algorithms for Fluids (Naval Research Laboratory, Washington). – Journal of Computational Physics, 31, 1979. – 335-362 p.
SUMMARY
The numerical scheme for the computation of a shock discontinuity developed by MacCormack has been extended to solve a number of differential equations, including cases explicitly containing higher-order derivatives. Comparisons with previous results are made, if available, to illustrate the advantages of the present method. The question of convergence of the numerical calculation is discussed. In the paper the author analyzes the stability of the scheme when the backward/forward steps are applied. Such principle will allow the full (one-dimensional) CFL limit on time step. This conjecture certainly has been verified again and again in numerous applications of the method, but has not been proved. The authors suggest a positive correlation between the accuracy and efficiency of a numerical method, pointing out that an explicit scheme operating at its maximum allowable time step has all the data needed to advance the solution, with a minimum of extraneous data. The purpose of this paper is to demonstrate the advantages of MacCormack scheme used earlier for the shock wave/laminar boundary layer interaction problem to more general fluid dynamics problems. The split explicit MacCormack scheme is applied to the inviscid equations of compressible flow to solve for the supersonic flow past symmetric diamond-shaped airfoils and double compression corners using simple, non-orthogonal, sheared meshes. They achieve results in excellent agreement with the exact (inviscid) solutions for these problems, demonstrating a reduction in computational time of more than a factor of two, relative to the unsplit method. The split method allows both: 1) advancing the solution at the full one-dimensional CFL limit in each space dimension, and 2) advancing the solution in the direction of the smaller mesh spacing multiple time steps for each time step in the coarser direction, allowing a better matching of the numerical and physical domains of dependence. The authors use three problems to illustrate three different points. The linear wave (advection) equation is used to show that the MacCormack explicit method reproduces the exact solution at a Courant number of unity due, the authors argue, to the alignment of the spacetime mesh with the solution for this value of Courant number. Second, the inviscid Burgers equation is used to show that, without corrective measures, the numerical scheme may capture (physically incorrect) expansion "shocks." Finally, the authors consider solutions of the Euler equations for several two-dimensional, supersonic flows, including flows past wedges, diamond airfoils, and a sphere. For these flows it is shown that the numerical error is reduced when the mesh is aligned with the shock position.
Список терминов
My research
My name is Valeria Korkishko. I graduated from Donetsk National University in 2014. Now I’m a post-graduate student of the Faculty of Physics and Technology. I’m a teacher of physics. I really love my job, I love the process of sharing my knowledge with other people. But I also have interests in science. My special subject is Computational Fluid Dynamics. My research deals with principals of modeling pulse and wave flows with mobile borders. I’m particularly interested in application of Mac-Cormack method to the high pulse fluid flows. One of the first tasks is to verify and if possible to amplify knowledge of possibility of application Mac-Cormack method to hydrodynamics method. I have been working at the problem for two years. I got interested in it when I was a student. My present work is based on the theory developed by my scientific adviser Alexandr Nikolaevich Semko. He has PHD at technical sciences. The title of his doctor’s dissertation was “Pulse and wave flows of liquid with mobile borders”. He proved it in 2006. Ten years after the problem hasn’t lost its topical significance. The title of my future dissertation is “Computational modeling of high pulse processes and technologies”. Pulse and wave flows with mobile borders meet in many physical processes bound to short-term and intensive influence on fluid, such as impact, explosion, electrical discharge etc. Dimensional redistribution of energy takes place in such kind of processes. It leads to sharp local increase of energy density. This effect is widely used in different installations and technological processes. Essential features of such processes are fugacity, high pressure, wave character and cavitation. Such flows are described by equations of non-stationary gas dynamics with appropriate initial and boundary conditions. Boundary conditions are often put on the specific borders. Motion laws of such borders are not known in advance and are a part of the decision of a problem. All these factors essentially complicate the decision of such issues. Therefore working out of the mathematical models adequately reflecting pulse and wave flows of fluid with mobile borders and cavitation is still the actual problem to which my research is devoted. Computational Fluid Dynamics (CFD) provides a qualitative (and sometimes even quantitative) prediction of fluid flows by means of mathematical modeling (partial differential equations), numerical methods (discretization and solution techniques) and software tools (solvers, pre- and post-processing utilities). CFD uses a computer to solve the mathematical equations for the problem at hand. At present there is a growing interest in improving the accuracy of numerical methods. CFD is a highly interdisciplinary research area, which lies at the interface of physics, applied mathematics and computer science. In computational fluid dynamics, the Mac-Cormack method is a widely used discretization scheme for the numerical solution of hyperbolic partial differential equations. This second-order finite difference method was introduced by Robert W. Mac-Cormack in 1969. The Mac-Cormack method is very elegant and easy to understand and program. It is well suited for nonlinear equations (inviscid Burgers equation, Euler equations, etc.) Unlike first-order upwind scheme, the Mac-Cormack does not introduce diffusive errors in the solution. However, it is known to introduce dispersive errors in the region where the gradient is high. In my research the theory of flux-corrected transport (FCT) developed by Boris and Book is extended to the numerical Mac-Cormack method in order to minimize dispersive errors. It has been established by recent studies that Mac-Cormacks method can be adequately applied to calculate liquid flows. So the scientific validity of my job is application of the Mac-Cormack method, widely used in gas dynamics, to liquid dynamics. My research is based on several steps. Initially, one must make mathematical model. Secondly, generation of cells, time instants, space and time discretization comes. Main part is software implementation and post-processing visualization. And after verification of model, the certain issues can be solved. Now I got more results in theoretical part rather than in practical use of obtained data. The obtained results agree with the previous findings.The problems are still far from being completely understood. I plan to finish my research work by the end of my study at the post-graduate course. I hope to get the degree of Candidate of Technical Science. By this time I will have got some publications in scientific periodicals. I think my dissertation will make a certain contribution to the knowledge of the subject by the discovery of new facts about the effectivity of Mac-Cormack’s method being applied to high pulse flows with mobile borders.
12 |
 напрямую вычисляется из частных дифференциальных уравнений и
напрямую вычисляется из частных дифференциальных уравнений и 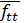 – определяется дифференцированием частных дифференциальных уравнений по времени.
– определяется дифференцированием частных дифференциальных уравнений по времени. , который опирается на разложение в ряд Тейлора первого порядка точности с дифференцированием по времени вперед для
, который опирается на разложение в ряд Тейлора первого порядка точности с дифференцированием по времени вперед для 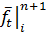 от исходной точки (i,n).
от исходной точки (i,n). +
+ 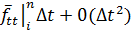
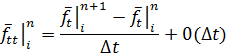
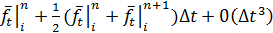
 и тогда уравнение примет форму
и тогда уравнение примет форму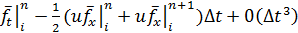
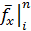 и
и  центрально-разностными аппроксимациями второго порядка точности и отбросив остаточные члены уравнения, получаем функциональное дифференциальное уравнение с порядком точности
центрально-разностными аппроксимациями второго порядка точности и отбросив остаточные члены уравнения, получаем функциональное дифференциальное уравнение с порядком точности  . Разностная расчетная сетка представлена на рис.2.1.
. Разностная расчетная сетка представлена на рис.2.1. , используя аппроксимации первого порядка с разностями «вперед» для величин
, используя аппроксимации первого порядка с разностями «вперед» для величин  ,
,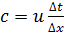 – параметр конвекции (в данном случае, число Куранта). На следующем шаге (корректора) уравнение решается оцениванием
– параметр конвекции (в данном случае, число Куранта). На следующем шаге (корректора) уравнение решается оцениванием  через аппроксимацию первого порядка в направлении «вперед» уравнения и оцениванием
через аппроксимацию первого порядка в направлении «вперед» уравнения и оцениванием  =
= 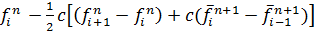
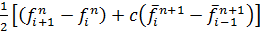
 . Однако при более глубоком рассмотрении ошибки дискретизации, порядок точности для метода Мак-Кормака оказывается равным
. Однако при более глубоком рассмотрении ошибки дискретизации, порядок точности для метода Мак-Кормака оказывается равным  .
. , устойчив при выполнении условия
, устойчив при выполнении условия  и конвергентен.
и конвергентен.