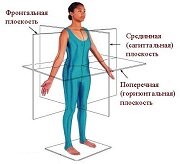
 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Эконометрический анализ при нарушении предпосылок метода наименьших квадратов
Основные понятия эконометрики. Вопросы: 7. Определение эконометрики и ее задачи. 8. Типы данных. 9. Терминология 10. Классификация экономических моделей. 11. Этапы экономического моделирования. 12. Виды зависимостей.
1. Эконометрика – это наука, изучающая количественные закономерности и взаимосвязи в экономике. Она зародилась и получила свое развитие на основе слияния экономической теории, математической экономики, экономической и математической статистики. В современной эконометрике широко используются информатика, статистические пакеты прикладных программ. Объект – экономика, различные экономические явления и взаимосвязи. Предмет – их количественные характеристики. Задачи: 1. построение эконометрических моделей и оценивание их параметров. 2. проверка гипотез, о свойствах показателей и формах их связей. Эконометрический анализ - основа для экономического анализа и прогнозирования.
2. Эконометрика базируется на реальных экономических данных. 2 типа данных: 1. пространственные данные – данные о каком-либо экономическом показателе, полученные от однотипных объектов и относящиеся к одному моменту (периоду времени). Модели, построенные по пространственным данным, называются пространственными моделями. 2. временные ряды – данные об экономическом показателе, характеризующем какой-либо объект в различные моменты времени. Модели, построенные на временных рядах , называются моделями временных рядов.
3. Исследуемый экономический показатель называют результативным, объясняемым, зависимым экономическим показателем. Соответствующую переменную – объясняемой или зависимой. Экономические показатели, воздействие которых на исследуемый экономический показатель изучается, называют факторами, объясняющими или независимыми показателями (переменными).
4. В эконометрике выделяют следующие основные 3 класса моделей: 1. Модели временных рядов: 1. Модели тренда (описывают устойчивые изменения экономического показателя в течение длительного времени). 2. Модели сезонности (описывают устойчивые внутригодовые колебания). 3. Модели авторегрессии (в них описываются влияния значения объясняемого экономического показателя в прошедший момент времени на его значение в текущий момент времени). 2. Регрессионные модели с одним уравнением. В них объясняемый экономический показатель представляется в виде функции от объясняющих экономических показателей (факторов). В зависимости от вида функции эти модели бывают: линейные и нелинейные. 3. Системы одновременных уравнений – это системы регрессионных уравнений, в которых в качестве объясняющих переменных используются объясняемые переменные из других уравнений системы.
5. 1 этап: постановочный. Формулируется цель исследования. Целью может служить анализ возможного развития экономического явления, прогноз экономических показателей, выработка на этой основе управленческих решений). 2 этап: априорный. Проводится анализ связей экономических переменных, выделяются зависимые и независимые переменные. 3 этап: информационный. Осуществляется сбор необходимой статистической информации о значениях экономических переменных. 4 этап: спецификация моделей. Для описания выявленных между экономическими показателями связей, подбирается математическая функция. 5 этап: параметризация. На основе собранных статистических данных об экономических переменных оцениваются параметры (коэффициенты) математических функций. 6 этап: верификация. Проводится проверка адекватности модели, т.е. насколько построенная модель соответствует реальному экономическому явлению.
6. Все зависимости между экономическими переменными можно разделить на 2 вида: 1. Функциональные. Если каждому значению независимой переменной или нескольким независимых переменных соответствует одно строго определенное значение зависимой переменной, то такая зависимость называется функциональной. В ней отсутствует воздействие случайных факторов, поэтому в экономике функциональная зависимость встречается редко. 2. Статистические. В экономике каждому значению независимых переменных может соответствовать несколько значений зависимой переменной в зависимости от воздействия неучтенных и случайных факторов. Например, пусть исследуется зависимость прибыли предприятия от объема производства и цены за единицу продукции. При одном и том же объеме производства и цене за единицу продукции прибыль предприятия может быть различна, т.к. на нее воздействуют множество других факторов, в том числе случайных. Зависимость между переменными, на которую накладывается воздействие случайных факторов, называется статистической. Для нее характерно то, что изменение независимой переменной приводит к изменению математического ожидания зависимой переменной. Уравнение регрессии – математическая формула, описывающая статистическую зависимость между переменными. Если формула описывается линейной функцией, то регрессия называется линейной. Если нелинейной функцией – нелинейной регрессией. Если регрессия связывает одну зависимую и одну независимую переменную, то такая регрессия называется парной (простой). Если рассматривается зависимость экономической переменной от нескольких экономических переменных, то такая регрессия называется множественной. Тема 2: Парная линейная регрессия Вопросы: 14. Истинное и выборочное уравнения регрессии. 15. Метод наименьших квадратов. 16. Геометрическая интерпретация метода наименьших квадратов. 17. Экономическая интерпретация коэффициентов парной линейной регрессии. 18. Основные предпосылки регрессионного анализа. Теорема Гаусса-Маркова. 19. Расчет стандартных ошибок коэффициентов регрессии. 20. Проверка значимости коэффициентов регрессии. 21. Построение доверительных интервалов для параметров теоретической регрессии. 22. Проверка общего качества уровня регрессии. Коэффициент детерминации. 23. Проверка значимости коэффициента детерминации. 24. Оценка тесноты связи между переменными. Коэффициент корреляции. 25. Проверка значимости коэффициента корреляции. 26. Прогнозирование.
1. Пусть исследуется статистическая зависимость экономического показателя У (объясняемая зависимая переменная) от экономического показателя Х (фактора, объясняющей или независимой переменной). Предположим, что зависимость носит линейный характер, тогда ее можно описать уравнением. У= где Х – неслучайная величина, У и Е – случайные величины. Случайная величина Е отражает воздействие на зависимую переменную У неучтенных и случайных факторов и называется ошибкой регрессии. Уравнение (1) называют истинным (теоретическим) уравнением регрессии или линейной регрессионной моделью. На основе реальных статистических данных об экономических показателях Х и У (выборке данных из генеральной совокупности) оцениваются параметры регрессии α и β и строится выборочное уравнение регрессии
а, в, - коэффициенты регрессии. Уравнение (2) называют еще эмпирическим уравнением регрессии. Одним из методов нахождения коэффициентов регрессии а и в является метод наименьших квадратов (МНК).
2. Пусть из генеральной совокупности выбраны данные об экономических показателях У: ( у
Разность между фактическими и расчетными значениями зависимой переменной обозначим ei и назовем остатком, т.е.:
Суть МНК заключается в следующем: коэффициенты а и в должны быть такими, чтобы сумма квадратов остатков была минимальна
в (5) уi и xi – известные величины, а а и в – неизвестные. Запишем необходимые условия экстремума функции S относительно а и в:
Система (6) является системой двух уравнений относительно двух неизвестных а и в. Она легко преобразовывается в систему (7):
Разделим оба уравнения системы на n:
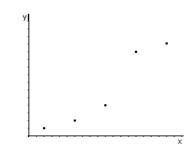
3. начертим оси координат Х ,У и изобразим в первой четверти точки (хi,уi)
Полученное изображение называется диаграммой рассеяния или полем корреляции. Проведем линию регрессии
Согласно МНК, а и в должны быть такими, чтобы построенная линия была ближайшей к точкам поля корреляции по их совокупности. Сумма квадратов расстояний от точек поля корреляции до линии регрессии должна быть минимальной. Пример1: исследуется зависимость прибыли предприятия от затрат на приобретение нового оборудования и техники. Собранны статистические данные по пяти однотипным предприятиям. Данные в млн. ден.ед. представлены в таблице 1.
Таблица 1
Построить уравнение регрессии. Данные таблицы представим графически, т.е. построим поле корреляции:
Из полученной диаграммы рассеяния видно, что зависимость статистическая и ее можно представить линейной регрессией
Таблица2 е нового оборудования и техники. в была минимальна
Подставим результаты, полученные в таблице 2 в формулы (8): испр.
Таким образом, уравнение регрессии, описывающее зависимость прибыли предприятия от затрат на новое оборудование и технику имеет вид:
Выбрав с помощью диаграммы рассеяния для описания зависимости линейную регрессию мы выполнили этап спецификации (подбора функции), а рассчитав коэффициенты а и в, т.е. оценив параметры теоретической регрессии, мы выполнили этап параметризации.
4. Коэффициент парной линейной регрессии в показывает, как в среднем изменяется зависимый экономический показатель у с изменением независимого фактора х на единицу. Так в примере 1 коэффициент в=0,775 показывает, что при увеличении расходов на приобретение нового оборудования и техники на 1 ден.ед. прибыль предприятия в среднем увеличится на 0,775 ден. ед. Коэффициент а парной линейной регрессии экономического смысла не имеет.
5. Для того, чтобы оценки параметров теоретической регрессии, полученные на основе МНК были лучшими по сравнению с оценками, найденными с помощью других методов, должны выполнятся определенные условия, которые называются основными предпосылками регрессионного анализа. Для того, чтобы их сформулировать, вспомним что теоретическая регрессия описывается уравнением
или для i-го наблюдения
Предпосылки: 1. Математическое ожидание случайного члена ε в любом наблюдении должно быть равно 0:
2. Дисперсия случайного члена ε должна быть постоянной для всех наблюдений:
3. Случайные члены должны быть статистически независимы друг от друга:
4. Объясняющая переменная хi – неслучайная величина Теорема Гаусса-Маркова: Если выполняются предпосылки 1-4 регрессионного анализа, то оценки параметров теоретической регрессии а и в есть наилучшие линейные оценки, обладающие следующими свойствами: 1. Они являются несмещенными:
2. Они являются эффективными, т.е. имеют наименьшую дисперсию в классе всех несмещенных оценок.
3. Они являются состоятельными, т.е.
Это значит, что при достаточно большом объеме выборки n, оценки а и в близки к истинным параметрам линейной регрессионной модели α и β.
6. Для расчета дисперсий D(a) и D(в) коэффициентов регрессии а и в в формулах (9) использовалась дисперсия σ2 случайного члена ε. Эта дисперсия неизвестна, но ее можно оценить, используя выборочные данные. Можно доказать, что несмещенной оценкой дисперсии σ2 является величина S2, где:
Величина S называется стандартной ошибкой регрессии. Она служит мерой разброса зависимой переменной около линии регрессии. Запишем в формулах (9) дисперсию σ2 ее оценкой S2:
Вернемся в Примеру 1 и рассчитаем стандартные ошибки коэффициентов регрессии:
7. Коэффициента регрессии получены на основании выборочных данных, отобранных случайным образом. Следовательно, коэффициенты регрессии а и в являются случайными числами и их значение может быть лишь случайно оказались отличными от нуля. Поэтому проводят проверку значимости коэффициентов регрессии, т.е. проверку того, значимо ли они отличны от нуля. Для этого используют процедуру проверку гипотез. Проверим значимость коэффициента в. Для этого: 1. Сформулируем гипотезу Н0:
Она состоит в том, что истинный коэффициент β=0, 2. В качестве критерия проверки гипотезы принимают случайную величину t:
Эта случайная величина имеет распределение Стьюдента с ν = n-2 степенями свободы. Подставим в формулу (12) оцененное по выборке значение коэффициента в и его стандартную ошибку Sв, получим наблюдаемое или расчетное значение t-критерия tрасч. 3. Выбирают уровень значимости проверки гипотезы. Как правило α= 0,05 или α=0,01, т.е. пятипроцентный или однопроцентный уровень значимости. 4. По таблице распределения Стьюдента для выборочного уровня значимости α/2 и ν = n-2 находят t кр. (критическое). 5. Если | tрасч.| > t кр., то гипотеза Н0 о равенстве параметра β=0 отвергается, параметр β существенно отличен от нуля, коэффициент в значим, а переменная х оказывает существенное влияние на зависимую у (Н0 считается неверной с вероятностью 1- α) 6. Если | tрасч.| < t кр., гипотеза Н0 принимается, коэффициент в незначим и переменная х не оказывает существенного влияния на зависимую переменную у. Замечание: аналогично проверяется значимость коэффициента а в уравнении регрессии, однако проверка значимости коэффициента в имеет гораздо большее значение в регрессионном анализе. Вернемся в примеру 1 и проверим значимость коэффициента в. Зависимость прибыли предприятия от расходов на новое оборудование и технику описывается регрессией:
(1,65) (0,143). 1. Формулируем гипотезу Н0, состоящую в том, что истинный коэффициент β=0, 2. Определим tрасч.
3. Выбираем уровень значимости проверки гипотезы α= 0,05. 4. По таблице распределения Стьюдента для α/2=0,025 и числа степеней свободы ν = 5-2=3 определим t кр. = 3,182. 5. | tрасч.|=5,4 > t кр.=3,182, поэтому гипотеза Н0 не верна с вероятностью 1-α= 1-0,05 = 0,95, параметр β существенно отличен от нуля, коэффициент в значим и затраты на новое оборудование и технику оказывают существенное влияние на прибыль предприятия.
8.
Вспомним, что линейная регрессионная модель (истинная или теоретическая регрессия) имеет вид:
На основании выборки строится выборочное уравнение регрессии:
Также на основании выборки рассчитывается стандартные ошибки регрессии Sa и Sв. Можно доказать, что с вероятностью 1-α (α – выбранный уровень значимости) значения параметра β лежат внутри интервала:
и с вероятностью 1-α (α – выбранный уровень значимости) значение параметра α истинной регрессии лежит внутри интервала:
Вернемся к Примеру 1 и построим доверительный интервал для параметра β в регрессионной модели, описывающей зависимость прибыли предприятия от затрат на новое оборудование и технику. Выберем уровень значимости α= 0,05. т.к. в данном примере ν = 5-2=3 , то t кр. = 3,182, в = 0,775,
Тогда с вероятностью 1-α= 1-0,05 = 0,95 параметр β истинной регрессии попадает в интервал
или 0,32<b<1,23 с вероятностью 95%.
9. Выборочное уравнение регрессии имеет вид:
тогда
Рассчитаем выборочную дисперсию (вариацию) Var(y):
Из основных предпосылок регрессионного анализа следует, что
т.е. дисперсия зависимой переменной у (Var(y)) распадается на 2 части:
Коэффициентом детерминации называют отношение R2:
которое характеризует долю вариации зависимой переменной, объясненную уравнением регрессии. Из (16) следует что R2 меняется от 0 до 1:
чем ближе R2 к единице, тем меньше
Вернемся к примеру 1, можно посчитать, что:
Коэффициент детерминации близок к 1, качество регрессии хорошее. Можно утверждать, что вариация (изменчивость) прибыли предприятия на 90,7% объясняется затратами на новое оборудование и технику и на 9,3% - прочими неучтенными и случайными факторами.
10. Т.к. R2 оценивается на основании выборочных данных, то его отличие от 0 может оказаться случайным. Поэтому проводят проверку его значимости: 1. Формулируется гипотеза Н0: R2=0, состоящая в том, что истинный коэффициент детерминации равен 0. 2. В качестве критерия проверки гипотезы применяют случайную величину F:
Величина F имеет распределение Фишера с двумя степенями свободы ν1=1, ν2=n-2. 3. Выберем уровень значимости проверки гипотезы значимости:
4. На основании α, ν1, ν2 в таблице распределения Фишера выбираем Fкр. (критическое) 5. Сравниваем Fрасч и Fкр.. если Fрасч > Fкр., то с вероятностью 1-α гипотезу Н0 считаем неверной, т.е. истинный коэффициент детерминации существенно отличен от нуля, уравнение регрессии значимо и переменные, включенные в уравнение регрессии достаточно объясняют поведение зависимой переменной. Если Fрасч < Fкр., то принимаемая гипотеза Н0, уравнение регрессии считается незначимым. Проверим значимость коэффициента детерминации в примере 1: 1. Формулируем гипотезу Н0: R2=0. 2. Находим Fрасч.. В (18) подставим значение коэффициента детерминации, оцененное по выборке:
3.Выбираем уровень значимости α=0,005. 4. В таблице распределения Фишера на основании α=0,05 и для степеней свободы ν1=1, ν2 =5-2=3 найдем Fкр.
6. Fрасч =29,2> Fкр.=10,13, поэтому Н0 не верна в вероятностью 1-0,05=0,95, коэффициент детерминации значим, значимо построенное в Примере 1 уравнение регрессии.
11.
Уравнение регрессии всегда дополняется показателем тесноты связи между переменными. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции:
rxy – безразмерная величина, показывает степень линейной зависимости между переменными. Чем ближе rxy к ±1, тем сильнее линейная зависимость. Чем ближе rxy к 0, тем линейная зависимость слабее. Если rxy = ±1, то имеет место функциональная линейная зависимость. Если rxy = 0, то линейная зависимость отсутствует. Если rxy >0, то связь между переменными положительная, если rxy <0 – отрицательная.
Рассчитаем коэффициент корреляции в примере 1:
rxy >0 и близок к 1 следовательно линейная зависимость между прибылью предприятия и затратами на новое оборудование – положительная и тесная.
12. Осуществляется аналогично проверки значимости коэффициентов регрессии и детерминации, используется t-статистика:
Проведем проверку значимости коэффициента корреляции в примере 1: 1. Формулируем гипотезу, состоящую в том, что истинный коэффициент корреляции равен нулю:
2. Подставим значение коэффициента корреляции, вычисленное по выборке в (20):
3. Выбираем уровень значимости α=0,05. 4. Для α/2=0,025 и для ν=n-2=3 в таблице распределения Стьюдента находим tкр.:
Следовательно, истинный коэффициент корреляции существенно отличен от 0, линейная зависимость между прибылью предприятия и затратами на новое оборудование и технику действительно тесная.. Замечание 1: В парном линейном регрессионном анализе проверка значимости коэффициента в, коэффициента корреляции и коэффициента детерминации являются эквивалентными. Замечание 2: Легко показать, что коэффициент детерминации равен квадрату коэффициента корреляции,
13. Прогнозирование на основе эконометрических моделей является одной из основных задач эконометрики. Под прогнозированием в эконометрике понимают построение оценки зависимой переменной для таких значений независимых переменных, которых нет в исходных наблюдениях. Различают точечное прогнозирование и интервальное. . Точечный прогноз это число, значение зависимой переменной, вычисляемое для заданных значений независимых переменных. Интервальный прогноз это интервал, в котором с заданным уровнем значимости ( с заданной вероятностью) находится истинное значение зависимой переменной для заданных значений независимых переменных. Рассмотрим парную линейную регрессионную модель Точечным прогнозом для ур является Ошибкой предсказания (
Можно доказать, что дисперсия ошибки предсказания
Из (21) следует, что чем ближе заданное значение независимой переменной Заменив в (21) дисперсию
Выберем уровень значимости α и по таблице распределения Стьюдента найдем tкр. Тогда с вероятностью 1- α истинное значение переменной ур будет находится внутри интервала:
Очевидно, что чем ближе Вернемся в Примеру 1 и найдем точечный и интервальный прогнозы для прибыли предприятия для затрат на новое оборудование и технику в размере 20 млн. денежных единиц.
Вывод: с вероятностью 0,95 истинное значение прибыли попадет в полученный интервал. Тема 3: Нелинейная регрессия. Вопросы: 5. Регрессии, нелинейные по переменным. 6. Регрессии, нелинейные по параметрам. 7. Индекс корреляции и индекс детерминации. 8. Эластичность функции.
Многие экономические зависимости не являются линейными по своей сути и их моделирование линейными регрессиями не дает положительного результата. Так для описания зависимости спроса на некоторый товар от его цены наиболее целесообразно использовать логарифмическую модель. При анализе зависимостей издержек от объема выпуска наиболее обоснованной является полиномиальная модель. Широко используемая функция Кобба-Дугласа, является степенной функцией
У – объем выпуска. К-затраты капитала. L - затраты труда. А, α, β – параметры. В современной экономике применяются также достаточно часто обратные и экспоненциальные модели. Различают регрессии нелинейные по переменным и нелинейные по параметрам.
1. К регрессиям, нелинейным по переменным относят полиномы различных степеней.:
равносторонняя гипербола функции вида Нелинейность по переменным устраняется путем замены переменной. Так в регрессии (1) сделаем замену х=х1, х2=х2 и получим двухфакторную линейную регрессию.
В уравнении (3) замена переменной имеет вид: Применение метода МНК для оценки коэффициентов соответствующих выборочной регрессии приводит к следующим системам уравнений. Для регрессии (!):
Для равносторонней гиперболы система уравнений имеет вид:
Для уравнения (4):
1. Полином третьей степени уравнения (2) часто моделирует зависимость общих издержек У от объема выпуска Х. график имеет вид:
2. Полином второй степени (уравнение (1)) парабола может описать зависимость между объемом выпуска Х и средними (либо предельными) издержками У
3. Гипербола (3) (обратная модель) применяется в тех случаях, когда неограниченное увеличение объясняющей переменной Х асимптотически приближает зависимую переменную У к некоторому пределу. Если а и в - оценки параметров гиперболы соответственно, то в зависимости знаков а и в возможны следующие ситуации:
рис.1 рис.2 рис.3 График на рисунке 1 может отражать зависимость между объемом выпуска Х и средними фиксированными издержками У. график на рисунке 2 может описывать зависимость между доходом Х и спросом на блага У. Такие функции называются функциями Тронквиста. Важным приложением графика на рисунке 3 является кривая Филипса, отражающая зависимость между уровнем безработицы Х (%) и процентным изменением заработной платы У. 4. Уравнения с квадратными корнями (4) использовались в исследовании урожайности и трудоемкости с/х производства. Пример 1: На основании информации о норме безработицы и темпах инфляции (таблица 1) построить : 1. диаграмму рассеяния. 2. уравнение регрессии, описывающее зависимость темпов инфляции от нормы безработицы.
Таблица 1
Строим диаграмму рассеяния:
Из диаграммы рассеяния видно, что зависимость можно описать гиперболой
Обратимся в Excel к программе регрессия и введем данные zi,
Замечание: Для оценки коэффициентов гиперболы можно построить систему уравнений (6) и решить ее.
2. К нелинейным по параметрам регрессиям относятся: степенная: показательная экспоненциальную Нелинейные по параметрам регрессии сводятся к линейным путем логарифмирования.
(8’) (9’) (10’)
Для нахождения оценок соответствующих коэффициентов выборочных регрессии для (8’), (9’),(10’) используется МНК при условии, что Пример 2: В таблице 2 приведены данные о расходах на питание и доходах 5 групп населения. Построить степенную регрессию, описывающую зависимость расходов на питание У от доходов населения Х. Таблица 2
Степенная регрессия имеет вид:
Получим линейное уравнение. Обратимся к программе «Регрессия», введем данные столбцов v и z, получим:
Выполним обратные преобразования (пропотенцируем полученное уравнение):
Замечание: Для построения регрессии (11) можно воспользоваться формулами (8) темы 2.
3. Уравнение нелинейной регрессии также как и линейной дополняются показателями корреляции и детерминации. Для оценки тесноты связи между переменными рассчитывается индекс корреляции:
Индекс корреляции (R) меняется от 0 до 1. чем ближе R к 1, тем сильнее нелинейная связь между переменными. Величина
используется для оценки качества уравнения регрессии. Для проверки значимости индекса детерминации используется F-статистика
n – объем выборки m – число параметров при независимых переменных. Так для параболы m=2, а для степенной функции m=1 4. В экономическом анализе часто используется эластичность функции. Эластичность функции
Эластичность показывает, насколько процентов изменяется функция Для степенной функции
В примере 2 степенная регрессия Для остальных функций эластичность не является постоянной величиной. Так для линейной функции
Рассчитаем коэффициент эластичности в примере 1 темы 2:
Можно утверждать, что с увеличением расходов на новое оборудование на 1%, прибыль предприятия возрастет на 1,29%. Тема 4: Множественная регрессия. Вопросы: 4. Оценка параметров линейной модели множественной регрессии. 5. Оценка качества множественной линейной регрессии. 6. Анализ и прогнозирование на основе многофакторных моделей.
Множественная регрессия является обобщением парной регрессии. Она используется для описания зависимости между объясняемой (зависимой) переменой У и объясняющими (независимыми) переменными Х1,Х2,…,Хk. Множественная регрессия может быть как линейная, так и нелинейная, но наибольшее распространение в экономике получила линейная множественная регрессия. 1. Теоретическая линейная модель множественной регрессии имеет вид:
соответствующую выборочную регрессию обозначим:
Как и в парной регрессии случайный член ε должен удовлетворять основным предположениям регрессионного анализа. Тогда с помощью МНК получают наилучшие несмещенные и эффективные оценки параметров теоретической регрессии. Кроме того переменные Х1,Х2,…,Хk должны быть некоррелированы (линейно независимы) друг с другом. Для того, чтобы записать формулы для оценки коэффициентов регрессии (2), полученные на основе МНК, введем следующие обозначения:
Тогда можно записать в векторно-матричной форме теоретическую модель:
и выборочную регрессию
МНК приводит к следующей формуле для оценки вектора
Для оценки коэффициентов множественной линейной регрессии с двумя независимыми переменными
Как и в парной линейной регрессии для множественной регрессии рассчитывается стандартная ошибка регрессии S:
и стандартные ошибки коэффициентов регрессии:
значимость коэффициентов проверяется с помощью t-критерия.
имеющего распространение Стьюдента с числом степеней свободы v=n-k-1.
2. Для оценки качества регрессии используется коэффициент (индекс) детерминации:
чем ближе Для проверки значимости коэффициента детерминации используется критерий Фишера или F- статистика.
с v1 =k, v2=n-k-1 степенями свободы. В многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Для компенсации такого увеличения вводится скорректированный (или нормированный) коэффициент детерминации:
Если увеличение доли объясняемой регрессии при добавлении новой переменной мало, то Пример 4: Пусть рассматривается зависимость прибыли предприятия от затрат на новое оборудование и технику и от затрат на повышение квалификации работников. Собраны статистические данные по 6 однотипным предприятиям. Данные в млн. ден. ед. приводятся в таблице 1.
Таблица 1
Построить двухфакторную линейную регрессию
Транспонируем матрицу Х:
Обращение этой матрицы:
таким образом зависимость прибыли от затрат на новое оборудование и технику и от затрат на повышение квалификации работников можно описать следующей регрессией:
Используя формулу (5), где k=2 рассчитаем стандартную ошибку регрессии S=0,636. Стандартные ошибки коэффициентов регрессии рассчитаем, используя формулу (6):
Аналогично:
Проверим значимость коэффициентов регрессии а1, а2. посчитаем tрасч.
Выберем уровень значимости
значит коэффициент а1 значим. Оценим значимость коэффициента а2:
Коэффициент а2 незначим. Рассчитаем коэффициент детерминации по формуле (7)
т.о. коэффициент детерминации значим, уравнение регрессии значимо.
3. Большое значение в анализе на основе многофакторной регрессии имеет сравнение влияния факторов на зависимый показатель у. Коэффициенты регрессии для этой цели не используется, из-за различий единиц измерения и различной степени колеблемости. От этих недостатков свободные коэффициенты эластичности:
Эластичность показывает, на сколько процентов в среднем изменяется зависимый показатель у при изменении переменной
вектор прогнозных значений независимых переменных, тогда точечный прогноз
или
Стандартная ошибка предсказания в случае множественной регрессии определяется следующим образом:
Выберем уровень значимости α по таблице распределения Стьюдента. Для уровня значимости α и числа степеней свободы ν = n-k-1 найдем tкр. Тогда истинное значение ур с вероятностью 1- α попадает в интервал:
Тема 5: Временные ряды. Вопросы: 4. Основные понятия временных рядов. 5. Основная тенденция развития – тренд. 6. Построение аддитивной модели.
1.
Временные ряды представляют собой совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Момент (или период) времени обозначают t, а значение показателя в момент времени обозначают у(t) и называют уровнем ряда. Каждый уровень временного ряды формируется под воздействием большого числа факторов, которые можно разделить на 3 группы: Длительные, постоянно действующие факторы, оказывающие на изучаемое явление определяющее влияние и формирующие основную тенденцию ряда – тренд T(t). Кратковременные периодические факторы, формирующие сезонные колебания ряда S(t). Случайны факторы, которые формируют случайные изменения уровней ряда ε(t). Аддитивной моделью временного ряда называется модель, в которой каждый уровень ряда представлен суммой тренда, сезонной и случайной компоненты:
Мультипликативная модель – это модель, в которой каждый уровень ряда представляет собой произведение перечисленных компонент:
Выбор одной из моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний примерно постоянна, то строят аддитивную модель. Если амплитуда возрастает, то мультипликативную модель. Основная задача эконометрического анализа заключается в выявлении каждой из перечисленных компонент.
2. Основной тенденцией развития (трендом) называют плавное и устойчивое изменение уровней ряда во времени свободное от случайных и сезонных колебаний. Задача выявления основных тенденций развития называется выравниванием временного ряда. К методам выравнивания временного ряда относят: 1) метод укрупнения интервалов, 2) метод скользящей средней, 3) аналитическое выравнивание. 1) Укрупняются периоды времени, к которым относятся уровни ряда. Затем по укрупненным интервалам суммируются уровни ряда. Колебания в уровнях, обусловленные случайными причинами, взаимно погашаются. Более четко обнаружится общая тенденция. 2) Для определения числа первых уровней ряда рассчитывается средняя величина. Затем рассчитывается средняя из такого же количества уровней ряда, начиная со второго уровня и т.д. средняя величина скользит по ряду динамики, продвигаясь на 1 срок (момент времени). Число уровней ряда, по которому рассчитывается средняя, может быть четным и нечетным. Для нечетного скользящую среднюю относят к середине периода скольжения. Для четного периода нахождение среднего значения не сопоставляют с определением t, а применяют процедуру центрирования, т.е. вычисляют среднее из двух последовательных скользящих средних. 3) Построение аналитической функции, характеризующей зависимость уровня ряда от времени. Для построения трендов применяют следующие функции:
Параметры трендов определяются с помощью МНК. Выбор наилучшей функции осуществляется на основе коэффициента R2.
3. Построение аддитивной модели проведем на примере. Пример 7: И |
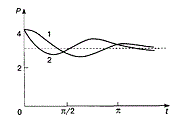
 +
+  Х+Е
Х+Е  (1),
(1), , (2)
, (2)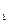 , у
, у  , …, у
, …, у  ) и Х: ( х
) и Х: ( х  . Если в (2) подставить наблюдаемое (выборочное значение хi, то получим расчетное значение
. Если в (2) подставить наблюдаемое (выборочное значение хi, то получим расчетное значение  зависимой переменной у:
зависимой переменной у: (3)
(3) (4)
(4)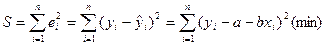 (5)
(5)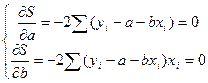 (6)
(6)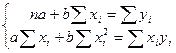 (7)
(7) (8)
(8)


 . Для оценки коэффициентов регрессии а и в воспользуемся формулами (8), для этого построим рабочую таблицу 2.
. Для оценки коэффициентов регрессии а и в воспользуемся формулами (8), для этого построим рабочую таблицу 2.
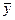






 ,
,




 (9)
(9)
 (10)
(10) (11)
(11) и
и  называют оценками дисперсии коэффициентов регрессии, а величина Sa и Sв – стандартными ошибками коэффициентов регрессии. Они используются для построения доверительных интервалов, которым принадлежат параметры истинной регрессии и для проверки значимости коэффициентов регрессии.
называют оценками дисперсии коэффициентов регрессии, а величина Sa и Sв – стандартными ошибками коэффициентов регрессии. Они используются для построения доверительных интервалов, которым принадлежат параметры истинной регрессии и для проверки значимости коэффициентов регрессии.
 .
. . (12)
. (12) .
.
 (15)
(15)



 .
. , следовательно
, следовательно
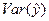 - часть, объясняемая уравнением регрессии, и часть
- часть, объясняемая уравнением регрессии, и часть  - необъяснимая часть, зависящая от неученых и случайных факторов.
- необъяснимая часть, зависящая от неученых и случайных факторов. , (16)
, (16) ,
, (17)
(17)
 . (18)
. (18) .
. .
. .
. , (19)
, (19)




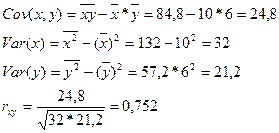
 (20)
(20) .
.

 ,
, .
. , т.е. чтобы получить точечный прогноз нужно в построенное уравнение регрессии подставить заданное значение независимой переменной.
, т.е. чтобы получить точечный прогноз нужно в построенное уравнение регрессии подставить заданное значение независимой переменной. ) называют разность между прогнозным и истинным значениями независимой переменной.
) называют разность между прогнозным и истинным значениями независимой переменной.
 . (21)
. (21) к
к  тем меньше дисперсия прогноза и чем больше объем выборки n, тем меньше дисперсия прогноза.
тем меньше дисперсия прогноза и чем больше объем выборки n, тем меньше дисперсия прогноза. на ее оценку
на ее оценку  , извлечем, квадратный корень и получим стандартную ошибку предсказания
, извлечем, квадратный корень и получим стандартную ошибку предсказания 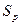 .
.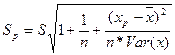 (22)
(22) (23)
(23)
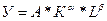
 (1)
(1) , (2)
, (2) , (3)
, (3) (4)
(4)
 , а в (4) -
, а в (4) -  .
. (5).
(5). (6)
(6) (7)
(7)





 . Сделаем замену переменных
. Сделаем замену переменных 
 , получим:
, получим:
 , (8)
, (8) , (9)
, (9) . (10)
. (10)
 распределен нормально.
распределен нормально.

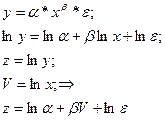
 (11)
(11)
 (12)
(12)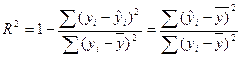 (13)
(13)
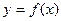 рассчитывается как относительное изменение у к относительному изменению х:
рассчитывается как относительное изменение у к относительному изменению х: (15)
(15) эластичность представляет собой постоянную величину, равную в, действительно:
эластичность представляет собой постоянную величину, равную в, действительно:
 описывает зависимость расходов на питание от доходов. Коэффициент 0,35 экономического смысла не имеет, а коэффициент в, равный 1,183, показывает, что увеличение личного дохода на 1% приведет к увеличению расходов на питание в среднем на 1,183%.
описывает зависимость расходов на питание от доходов. Коэффициент 0,35 экономического смысла не имеет, а коэффициент в, равный 1,183, показывает, что увеличение личного дохода на 1% приведет к увеличению расходов на питание в среднем на 1,183%. эластичность
эластичность  , т.е. эластичность зависит от х, поэтому для остальных функций вычисляется средний показатель эластичности, в частности для линейной функции по формуле:
, т.е. эластичность зависит от х, поэтому для остальных функций вычисляется средний показатель эластичности, в частности для линейной функции по формуле: (16)
(16)
 (1)
(1) (2)
(2)

 .
. коэффициентов выборочной регрессии:
коэффициентов выборочной регрессии: (3)
(3) , можно решить систему уравнений:
, можно решить систему уравнений: (4)
(4) (5)
(5) (6)
(6) (7)
(7) , (8)
, (8) к 1, тем выше качество регрессии.
к 1, тем выше качество регрессии. (9)
(9)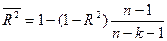 (10)
(10) может уменьшиться. Значит, добавлять новую переменную нецелесообразно.
может уменьшиться. Значит, добавлять новую переменную нецелесообразно.





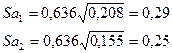

 , число степеней свободы
, число степеней свободы

 . Прибыль предприятия на 96% зависит от затрат на новое оборудование и технику и повышение квалификации на 4% от прочих и случайных факторов. Проверим значимость коэффициента детерминации. Рассчитаем Fрасч.:
. Прибыль предприятия на 96% зависит от затрат на новое оборудование и технику и повышение квалификации на 4% от прочих и случайных факторов. Проверим значимость коэффициента детерминации. Рассчитаем Fрасч.:
 (11)
(11) на 1% при условии неизменности значений остальных переменных. Чем больше
на 1% при условии неизменности значений остальных переменных. Чем больше  , тем больше влияние соответствующей переменной. Как и в парной регрессии для множественной регрессии различают точечный прогноз и интервальный прогноз. Точечный прогноз (число) получают при подстановке прогнозных значений независимых переменных в уравнение множественной регрессии. Обозначим через:
, тем больше влияние соответствующей переменной. Как и в парной регрессии для множественной регрессии различают точечный прогноз и интервальный прогноз. Точечный прогноз (число) получают при подстановке прогнозных значений независимых переменных в уравнение множественной регрессии. Обозначим через: (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16) . (1)
. (1) . (2)
. (2)