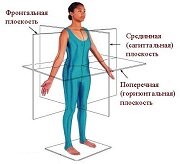
 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задание Д-13. Исследование равновесия
Механической системы методом обобщенных Координат Схемы находящихся в равновесии механизмов показаны на рис. 54−58, а необходимые данные приведены в табл. 10. Применяя метод обобщенных координат и пренебрегая силами сопротивления, определить величину, указанную в предпоследнем столбце табл. 10. Примечание. Механизмы в вариантах 3, 6, 10, 14, 16, 18, 19, 25 и 30 расположены в вертикальной плоскости, а остальные — в горизонтальной. Пример выполнения задания (рис. 59).Дано: Определить величину момента Решение. Рассматриваемый механизм (рис. 67) , имеющий одну степень свободы, находится в равновесии под действием следующих активных силовых факторов: силы том Выберем в качестве обобщенной координаты q угол поворота Поскольку рассматриваемая система (механизм) обладает одной степенью свободы, условием равновесия ее в обобщенных координатах является равенство нулю обобщенной силы
Для определения обобщенной силы Q сообщим механической системе возможное перемещение из заданного ее положения; при этом обобщенная координата
Тогда
где
При рассматриваемом возможном перемещении кривошип ОА совершает поворот вокруг точки О против хода часовой стрелки на угол В соответствии с уравнением (2) получим
При определении обобщенной силы Чтобы найти выражение для обобщенной силы Из рис. 67 ясно, что
тогда
Так как Сила упругости пружины пропорциональна ее деформации:
При равновесии механизма из соотношения (1) следует
Откуда искомый уравновешивающий момент
Ответ:
Задание Д-14. Применение метода обобщенных |
 Н, с=100Н/см;
Н, с=100Н/см;  см;
см;  см;
см;  см;
см; , уравновешивающего находящийся в горизонтальной плоскости механизм в данном положении, если известно, что пружина растянута на
, уравновешивающего находящийся в горизонтальной плоскости механизм в данном положении, если известно, что пружина растянута на  см.
см. ,пары сил с момен-
,пары сил с момен- как реакцию неидеальной связи учитываем наряду с активными силами. Остальные наложенные на механизм связи яв- ляются идеальными и поэтому их реакции на расчетной схеме не показываются.
как реакцию неидеальной связи учитываем наряду с активными силами. Остальные наложенные на механизм связи яв- ляются идеальными и поэтому их реакции на расчетной схеме не показываются. кривошипа ОА (рис. 67, а). В данном положении механизма
кривошипа ОА (рис. 67, а). В данном положении механизма 
 , соответствующей выбранной обобщенной координате:
, соответствующей выбранной обобщенной координате: . (1)
. (1) получит приращение
получит приращение  .
. Рис. 67
Рис. 67 , (2)
, (2) −сумма элементарных работ активных сил и реакций неидеальных связей на соответствующих возможных перемещениях их точек приложения;
−сумма элементарных работ активных сил и реакций неидеальных связей на соответствующих возможных перемещениях их точек приложения; − вариация выбранной обобщенной координаты.
− вариация выбранной обобщенной координаты. ; звено АВ − на угол
; звено АВ − на угол  вокруг мгновенного центра скоростей Р этого звена; звено ВС − на угол
вокруг мгновенного центра скоростей Р этого звена; звено ВС − на угол  вокруг точки
вокруг точки  . Модули возможных перемещений точек В
. Модули возможных перемещений точек В  и С приложения сил
и С приложения сил  и
и 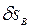 и
и  .
. . (3)
. (3) ;
;  ,
, .
. , то
, то  .
. . Подставив в уравнение (3) выражения для силы
. Подставив в уравнение (3) выражения для силы  и возможных перемещений
и возможных перемещений  .
.

 Н·м.
Н·м. кН·м.
кН·м.