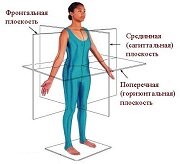
ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Классическое определение вероятности
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Министерство образования Республики Башкортостан Государственное автономное профессиональное образовательное учреждение «Ишимбайский нефтяной колледж»
КУРС ЛЕКЦИИ ПО РАЗДЕЛУ МАТЕМАТИКИ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ» Составитель: Ишемгулов А.Ф., преподаватель математики
Ишимбай 2016 Случайные события Основные понятия теории вероятностей Изучение каждого явления в порядке наблюдения или выполнения опыта связано с выполнением некоторого комплекса условий, или испытанием. Всякий результат или исход испытания называется событием. Так, событиями являются: поражение и не поражение мишени в результате произведённого выстрела (испытания); выигрыш и др. Для обозначения событий приняты первые буквы латинского алфавита А, В, С и т.д. События подразделяются на следующие три вида: достоверные, невозможные и случайные. Достоверным называется событие, которое в результате испытания обязательно произойдёт. Так, достоверным событием является извлечение белого шара из урны, в которой все шары белые. Невозможным называется событие, которое в результате испытания заведомо не произойдёт. Так, невозможным событием является извлечение чёрного шара из урны, в которой все шары белые. Случайнымназывается событие, которое в результате испытания либо произойдёт, либо не произойдёт. Так, случайным событием является поражение мишени при одном выстреле из ружья. Случайные события подразделяются на совместные и несовместные. События А, В, С называются несовместными, если в условиях испытания каждый раз возможно появление только одного из них. Так, если брошена монета, то события «появился герб» и «появилась надпись» - несовместные. События А, В, С называются совместными, если в данных условиях появление одного из этих событий не исключает появления другого при том же испытании. Так, при одновременной стрельбе из двух винтовок поражения мишеней являются совместными событиями. Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Пример. Стрелок произвёл выстрел по цели. Обязательно произойдёт одно из следующих двух событий: попадание, промах. Эти два несовместных события образуют полную группу. События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другие. Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначить через А, то другое принято обозначать . Попадание и промах при выстреле по цели – противоположные события. Если А – попадание, то - промах. Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Так, например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то А+В – попадание при первом выстреле, или при втором, или в обоих выстрелах. Произведение двух событий А и В называют событие АВ, состоящее в совместном появлении этих событий. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А – стандартная деталь, В - деталь завода №1, то АВ – стандартная деталь завода №1. Элементарным исходом называется каждый из возможных результатов испытания. Те элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию.
Классическое определение вероятности Вероятность – одно из основных понятий теории вероятностей. Приведём определение, которое называется классическим. Рассмотрим пример. Пусть в урне содержатся 6 одинаковых, тщательно перемешанных шаров, причём 2 из них – красные, 3 – синие и 1 – белый. Поставим перед собой задачу дать количественную оценку возможности того, что взятый наудачу шар цветной. Обозначим А – появление цветного шара. В нашем примере возможны следующие 6 элементарных исходов: ω1 – появился белый шар, ω2 , ω3 – появился красный шар, ω4 , ω5 , ω6 – появился синий шар. Эти исходы образуют полную группу попарно несовместных событий и они равновозможны. Благоприятствуют нашему событию А следующие 5 исходов: ω2 , ω3, ω4 , ω5 , ω6. Таким образом, событие А наступит, если в испытании наступит один, безразлично какой, из элементарных исходов, благоприятствующих А. Отношение числа благоприятствующих событию А элементарных исходов к их общему числу называют вероятностью события А и обозначают через p. В нашем примере всего элементарных исходов 6; их них благоприятствующих появлению события А – 5. Следовательно, вероятность того, что взятый шар окажется цветным, равна р(А) = . Это число и даёт ту количественную оценку степени возможности появления цветного шара, которую мы хотели найти. Определение. Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу и определяется формулой , где – число элементарных исходов, благоприятствующих появлению события А; – число всех элементарных исходов испытания. Отметим следующие свойства: • Вероятность достоверного события равна единице. Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае и p. • Вероятность невозможного события равна нулю. Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае • Вероятность случайного события есть положительное число, заключённое между нулём и единицей. Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае < 1, следователь Итак, вероятность любого события удовлетворяет двойному неравенству . Пример 1. Среди 25 деталей, подвергаемых проверке, имеется всего 15 точных. Какова вероятность того, что из числа взятых наудачу 10 деталей окажется 8 точных? Количество всех равновозможных выборок по 10 деталей из 25 определяется по формуле = 3 268 760. Число же тех выборок по 10, в которых 8 точных деталей сочетаются с 2 неточными, определяется произведением Отсюда искомая вероятность
|