ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Свойства функции комплексного переменного
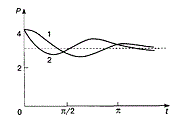
Для функции f(z) и g(z) справедливы следующие условия: 1) 2) 3) Функция W=f(z) называется непрерывной в точке Z0 если выполняется равенство Основные трансцендентные ф-ии Трансцендентными называются аналитические ф-ии,которые не являются алгебраическими . Если аргументом показательных тригонометрических ф-ий является комплексное число,то определение этих функций в элементарной алгебре теряет смысл! Пример: f (x)=sinx , : f (x)=sinx+x и т.д.
Производная функций комплексных переменных. Производная от однозначной функции W=f(z) в точке называется Функция f (z) имеющая производную в любой точке области D называется аналитической функцией на этой области (sh z)’= ch z (ch z)’=sh z
Свойства векторов. Линейная зависимость векторов. Вектором – называется направленный отрезок. Длинной (модулем) вектора называется расстояние между началом и концом вектора. Свойства: 1) 2) 3) 4) 5) 6) (α * β)* 7) (α + β)* 8) α *( 9) 1* Линейная зависимость векторов. Векторы Свойства линейно-зависимых векторов. 1)если среди аi есть нулевой вектор, то эти векторы линейно-зависимы. 2)если к системе линейно-зависимых векторов добавить один или несколько произвольных векторов, то полученная система будет линейно – зависимой 3)система векторов линейно-зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию других векторов 4) любые 2 коллинеарные вектора линейно-зависимы ,любые 2 линейно-зависимы вектора – коллинеарны 5)любые 4 вектора линейно-зависимы.
Скалярное произведение векторов. Скалярным произведением векторов | a * b =| свойства скалярного произведения:
(m*
Векторное произведение векторов Называется вектор С удовлетворяющий след. условиям: |c| = |a| * |b| * Sin Sin С oртагонален a и b C a, b, с образуют правую тройку веторов с = a * b = [ a * b ] = [ a * b ]
Смешанное произведение векторов Смешанным произведением упорядоченной тройки векторов a, b и c называется число <a, b, c>, т.ч. <a,b,c>=([a,b],c). <a,b,c>=Va,b,c, если a,b,c – правая тройка, или <a,b,c>= -Va,b,c, если a,b,c – левая тройка. Здесь Va,b,c – объём параллелепипеда, построенного на векторах a, b и c. (Если a, b и c компланарны, то Va,b,c=0.) В декартовой системе координат, если a={x1, y1, z1}, b={x2, y2, z2}, с={x3, y3, z3}, => <a,b,c>=
27. Градиент скалярного поля Ротор векторного поля Ротор (вихрь) векторного поля
или в символическом виде
29. Дивергенция векторного поля Дивергенцией (или расходимостью) дифференцируемого векторного поля
Это же выражение можно записать с использованием оператора набла
|
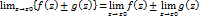
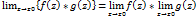
 ,
,  0
0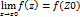
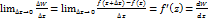
 =
=  -
- 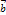 =
= 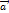 + (-
+ (- 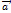
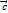 ) = (
) = ( 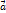 =α*(β *
=α*(β *  *
*  …..
…..  называется линейно-зависимыми, если существует такая линейная комбинация β1*
называется линейно-зависимыми, если существует такая линейная комбинация β1* 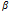 2*
2*  +…+
+…+ 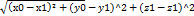
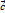 )=
)=  *
*  =
=  *
*  ,
,  >=0; 0<=
>=0; 0<=  <=П
<=П
 a и с
a и с  .
. , в котором произведение
, в котором произведение  имеет наибольшее значение.
имеет наибольшее значение. .
.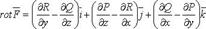
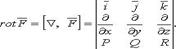
 называется скаляр
называется скаляр