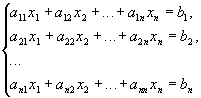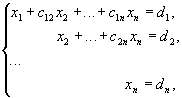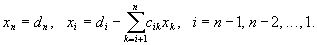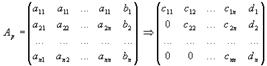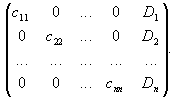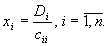ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основные действия над матрицей
Ели m=n, то такая матрица называется квадратной.
Е= 1 0 … 0 0 1 … 0 : : : 0 0 … 0 If Квадратная матрица вида- диагональная матрица
0 а22 … 0 : : : 0 0 … an3 Сложение и вычитание. Матрицы сводятся к собственным операциям над их элементами, самым главным свойством этих операций, является то, что они определены точно для матриц одинакового размера. Сумма или разность матриц является сумма или разность элементов исходных матриц.
C=A±B=B±A
32.Операция умножения матриц. Операция умножения или деления матрицы любого размера на произвольное число, сводится к умножению или делению каждого элемента матрицы на то число.
α а21 α а22 … α аmn2 : : : α amn α amn α amn
α(A±B)= αА± αB A(α±β)=αA±βA Произведение матриц называется матрица, элементы которой могут быть вычислены по формуле. С=A*B
Свойства операции умножения матрицы. 1)Умножение некоммутативно ab≠ba
а21 а22 0 1 а21 а22 2)Операция перемножения матриц ассоциативна, т.е. if определены АВ и (АВ)С, то определены произведения ВС и А(ВС) (АВ)С=А(ВС) 3) Операция умножения матриц дистрибутивно по отношению к сложению т.е. имеет смысл выражение. А(В+С) и (А+В)С то соответств А(В+С)=АВ+АС (А+В)С=АС+ВС 4) if произведение АВ определено, то для любого числа α верно соотношение. Α(АВ)=(αА)В=А(αВ) 5) If определено произведение АВ, то определено произведение
6)Для любых квадратных матриц детерминант произведения. det(АВ)=det*F*debt
33. Элементарные преобразования. Миноры 1)Умножение строки на часло отличное от “0” Операция умножения или деления матрицы любого размера на произвольное число, сводится к умножению или делению каждого элемента матрицы на то число.
α а21 α а22 … α аmn2 : : : α amn α amn α amn
α(A±B)= αА± αB A(α±β)=αA±βA 2)Транспонирование матриц. Матрицу В называют транспониравонной матрицей А, а переход от А к В транспонированием, if элементы каждой строки матрицы А записать в том же порядке в каждом столбце матрица В.
а21 а22 … а23 : : : an1 an2 an3
а21 а22 … а23 : : : an1 an2 an3 3) Определители( детерминанты) Определителем обратной матрицы А называется число, которое может быть вычислено по элементам матрицы по формуле detA=
В об случай (i=1,2,3…n) Определитель единичной матрицы равен единице.Для рассматриваемой матрицы А, число Дополнительные миноры существуют только в квадратных матрицах. Дополнительный минор, произвольная элемента квадратной матрицы
7 8 9 7 9
detА=( нахождение детерминанта)=0 Наиболее важным соотношением является 1)detA=det 2)det(A±B)=detA*debt 3)det(AB)=detA*debt 4)if в квадратной матрице поменять местами 2 строки и 2 столбца, то определитель матрицы изменит знак не изменившись по абсолютной величине. 5)При умножение столбца или строки на число, ее определитель умножается на это число. 6)If в матрице строки или столбцы линейно зависимы, то ее определитель =0
4 5 6 7 8 9 Столбцы или строки матрицы называются линейно зависимыми, if существует тих линейная комбинация, равная 0 , имеющее неравновесное решение.
7) if матрица содержит нулевой столбец, то ее определитель =0 8)Определитель матрицы не изменится, если к элементам из его строк или столбца прибавить , вычислить элементы др. строк или столбец умноженный на какое либо число ≠0 9)if для элементов какой либо строки или столбца матрицы верно соотношение D=d1±d2 ; e=e1±e2; f=f1±g2, то
d e f = d1 e1 f1 ± d2 e2 f2 k l m k l m k l m Минор: if в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то опред. Составленный из элементов расположенных на пересечение этих строк и столбцов называемая минором матрицы А. If выделено S строк и столбцов, то полученный минор называется минором порядка S.
Обратная матрица
Свойства обратной матрицы: 1) 2) 3)
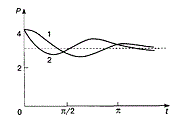
Метод Крамера Данный метод также применияется для системы линейных уравнений, где число переменных равно числу уравнений. Необходимо ввести ограничения на коэффициенты системы. То есть необходимо чтобы все уравнения были линейно независимы. Значит
Т.: Правило Крамера Система с n уравнениями и n неизвестными
Метод Гаусса Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Метод Гаусса (его еще называют методом гауссовых исключений) состоит в том, что совместную систему n линейных алгебраических уравнений относительно n неизвестных
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей
решение которой находят по рекуррентным формулам
В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными преобразованиями над строками приводят расширенную матрицу системы к ступенчатому виду:
а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась диагональная матрица
В результате получаем решение системы:
|
 Единичная матрица
Единичная матрица =0 if i≠j
=0 if i≠j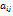 =
=  (
(  =
=  ) то такая матрица называется симметричной.
) то такая матрица называется симметричной. А= а11 0 … 0
А= а11 0 … 0 =
=  αА= α а11 α а12 … α аmn1
αА= α а11 α а12 … α аmn1 =
= 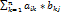 => Операция умножения матриц определена только для матриц, число столбцов 1-й матрицы из которых= числу 2-й матрицы.
=> Операция умножения матриц определена только для матриц, число столбцов 1-й матрицы из которых= числу 2-й матрицы.
 Однако если для каких либо матриц соотношение АВ=ВА выполняется, также матрицы называются перестановочными. Перестановочные могут быть только квадратные матрицы только одного и того же размера, порядка. АЕ=ЕА
Однако если для каких либо матриц соотношение АВ=ВА выполняется, также матрицы называются перестановочными. Перестановочные могут быть только квадратные матрицы только одного и того же размера, порядка. АЕ=ЕА А= а11 а12 * 1 0 = а11 а12
А= а11 а12 * 1 0 = а11 а12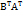
 =
=  αА= α а11 α а12 … α аmn1
αА= α а11 α а12 … α аmn1 А= а11 а12 … а13
А= а11 а12 … а13 В=
В= 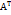 *= а11 а12 … а13
*= а11 а12 … а13 *
* 
 – det матрицы, полученный из исходной, вычерчиванием 1-й строки и k столбца.
– det матрицы, полученный из исходной, вычерчиванием 1-й строки и k столбца. каждый элемент матрицы свой дополнительный минор.
каждый элемент матрицы свой дополнительный минор. = определителю матрицы, полученной из исходной, вычерчиванием I строки и j столбца.
= определителю матрицы, полученной из исходной, вычерчиванием I строки и j столбца.
 1 2 3
1 2 3

 4 5 6 М22 = 1 3 = 9-21=-12
4 5 6 М22 = 1 3 = 9-21=-12 1 2 3
1 2 3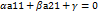
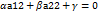
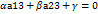


 a b c a b c a b c
a b c a b c a b c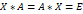
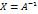
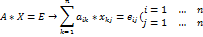
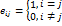
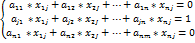
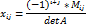
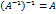
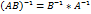
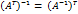
 необходимое условие.
необходимое условие. в случае если
в случае если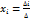 , где
, где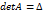
 - определительматрицы , получаемый из матрицы системы заменой i –столбца столбцом свободных членов
- определительматрицы , получаемый из матрицы системы заменой i –столбца столбцом свободных членов 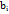
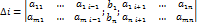
 (определитель матрицы системы отличен от нуля)
(определитель матрицы системы отличен от нуля)